题目内容
已知定义在R上的函数f(x)=x2(ax-3),其中a为常数.
(Ⅰ)若x=1是函数f(x)的一个极值点,求a的值;
(Ⅱ)若函数f(x)在区间(-1,0)上是增数,求a的取值范围.
(Ⅰ)若x=1是函数f(x)的一个极值点,求a的值;
(Ⅱ)若函数f(x)在区间(-1,0)上是增数,求a的取值范围.
解:(Ⅰ)a=2; (Ⅱ)a≥-2.
本试题主要是考查了导数在研究函数中的运用。
(1)根据f(x)=ax3-3x,f¢(x)=3ax2-6x=3x(ax-2),因为x=1是f(x)的一个极值点,∴f¢(1)=0得到参数a的值。
(2)函数f(x)在区间(-1,0)上是增数,说明导函数在给定区间恒大于等于零,既可以运用分离参数的思想求解得到参数的范围。
解:(Ⅰ)f(x)=ax3-3x,f¢(x)=3ax2-6x=3x(ax-2),。。。。。。。。。。。。。。。。。。
∵x=1是f(x)的一个极值点,∴f¢(1)=0,。。。。。。。。。。。。。。。。。。。。。。。。。
∴a=2; 。。。。。。。。。。。。。。。。。。。
(Ⅱ)①当a=0时,f(x)=-3x2在区间(-1,0)上是增函数,∴a=0符合题意;
②当a≠0时,f¢(x)=3ax(x-),由f¢(x)=0,得x=0,x=
当a>0时,对任意x∈(-1,0),f¢(x)>0,∴a>0符合题意;。。。。。。。。。。
当a<0时,当x∈(,0)时,由f¢(x)>0,得≤-1,∴-2≤a<0符合题意;。。
综上所述,a≥-2. 。。。。。
(1)根据f(x)=ax3-3x,f¢(x)=3ax2-6x=3x(ax-2),因为x=1是f(x)的一个极值点,∴f¢(1)=0得到参数a的值。
(2)函数f(x)在区间(-1,0)上是增数,说明导函数在给定区间恒大于等于零,既可以运用分离参数的思想求解得到参数的范围。
解:(Ⅰ)f(x)=ax3-3x,f¢(x)=3ax2-6x=3x(ax-2),。。。。。。。。。。。。。。。。。。

∵x=1是f(x)的一个极值点,∴f¢(1)=0,。。。。。。。。。。。。。。。。。。。。。。。。。

∴a=2; 。。。。。。。。。。。。。。。。。。。

(Ⅱ)①当a=0时,f(x)=-3x2在区间(-1,0)上是增函数,∴a=0符合题意;
②当a≠0时,f¢(x)=3ax(x-),由f¢(x)=0,得x=0,x=
当a>0时,对任意x∈(-1,0),f¢(x)>0,∴a>0符合题意;。。。。。。。。。。

当a<0时,当x∈(,0)时,由f¢(x)>0,得≤-1,∴-2≤a<0符合题意;。。

综上所述,a≥-2. 。。。。。


练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 .
. 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件;
上递增的充分而不必要的条件; 时,满足
时,满足 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的单调递减区间.
的单调递减区间.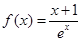 .
. 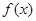 的单调区间;
的单调区间;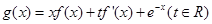 .是否存在实数
.是否存在实数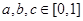 ,使得
,使得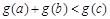 ?若存在,求实数
?若存在,求实数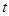 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
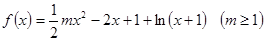 .
.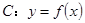 在点
在点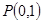 处的切线
处的切线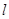 与曲线
与曲线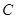 有且只有一个公共点,求
有且只有一个公共点,求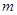 的值;
的值;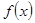 存在单调递减区间
存在单调递减区间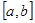 ,并求出单调递减区间的长度
,并求出单调递减区间的长度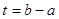 的取值范围.
的取值范围.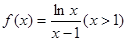
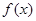 的单调性;
的单调性;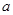 、使得关于
、使得关于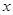 的不等式
的不等式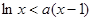 在(1,
在(1,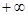 )上恒成立,若存在,求出
)上恒成立,若存在,求出 是减函数的区间为( )
是减函数的区间为( )


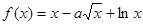 (
(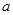 为常数)在定义域上是增函数,则实数
为常数)在定义域上是增函数,则实数