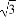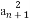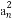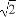题目内容
已知函数y=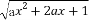
的定义域为R.
(1)求a的取值范围.
(2)若函数的最小值为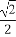
,解关于x的不等式x2-x-a2-a<0.
(1) 0≤a≤1 (2) {x|-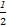
<x<
}
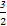【解析】(1)∵函数y=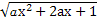
的定义域为R,
∴ax2+2ax+1≥0恒成立.
当a=0时,1≥0,不等式恒成立;
当a≠0时,则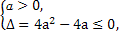
解得0<a≤1.
综上,0≤a≤1.
(2)因为函数的最小值为
,所以g(x)=ax2+2ax+1的最小值为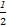,因此
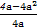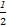=,解得a=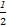,于是不等式可化为x2-x-
<0,即4x2-4x-3<0,解得-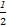<x<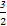,故不等式x2-x-a2-a<0的解集为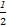{x|-<x<}.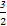
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
