题目内容
设二次函数f(x)=x2+bx+c,满足f(x+3)=f(3-x),则使f(x)>c-8的x的取值范围为( )
(A)(-∞,2) (B)(4,+∞)
(C)(-∞,2)∪(4,+∞) (D)(2,4)
C
【解析】∵f(x+3)=f(3-x),
∴x=3是y=f(x)的对称轴,
∴-
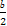=3,∴b=-6,
∴f(x)=x2-6x+c,
∴f(x)>c-8,即x2-6x+8>0,
解得x<2或x>4.
练习册系列答案
相关题目
题目内容
设二次函数f(x)=x2+bx+c,满足f(x+3)=f(3-x),则使f(x)>c-8的x的取值范围为( )
(A)(-∞,2) (B)(4,+∞)
(C)(-∞,2)∪(4,+∞) (D)(2,4)
C
【解析】∵f(x+3)=f(3-x),
∴x=3是y=f(x)的对称轴,
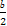∴-=3,∴b=-6,
∴f(x)=x2-6x+c,
∴f(x)>c-8,即x2-6x+8>0,
解得x<2或x>4.
