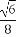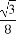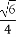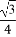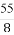Question

数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*,若数列{an}是等比数列,则实数t=　　　.

 

Answer 1

1

【解析】【思路点拨】得出关于an+1,Sn的式子,降低一个角标再得一个关于an,Sn-1的式子,两个式子相减后得出an+1,an的关系,可得数列{an}中,a2,a3,a4,…为等比数列,只要等于上面数列的公比即可.

【解析】
由题意得an+1=2Sn+1,

an=2Sn-1+1(n≥2),

两式相减得an+1-an=2an,即an+1=3an(n≥2),

所以当n≥2时,{an}是等比数列,

要使n≥1时,{an}是等比数列,则只需

==3,从而t=1.