题目内容
某公司有价值a万元的一条生产流水线,要提高该生产流水线的生产能力,就要对其进行技术改造,改造就需要投入资金,相应就要提高生产产品的售价.假设售价y万元与技术改造投入x万元之间的关系满足:
①y与a-x和x的乘积成正比;②x=
时y=a2;
③0≤
≤t其中t为常数,且t∈[0,1].
(1)设y=f(x),试求出f(x)的表达式,并求出y=f(x)的定义域;
(2)求出售价y的最大值,并求出此时的技术改造投入的x的值.
①y与a-x和x的乘积成正比;②x=
| a |
| 2 |
③0≤
| x |
| 2(a-x) |
(1)设y=f(x),试求出f(x)的表达式,并求出y=f(x)的定义域;
(2)求出售价y的最大值,并求出此时的技术改造投入的x的值.
(1)设y=k(a-x)x,当x=
时y=a2,可得k=4,∴y=4(a-x)x∴定义域为[0,
],t为常数,t∈[0,1]
(2)y=4(a-x)x=-4(x-
)2+a2
当
≥
时,即
≤t≤1,x=
时,ymax=a2
当
<
时,即0≤t<
时,y=4(a-x)在[0,
]上为增函数,
则当x=
时,ymax=
从而当
≤t≤1时,投入x=
时,售价y最大为a2万元;
当0≤t<
时,投入x=
时,售价y最大为
万元.
| a |
| 2 |
| 2at |
| 1+2t |
(2)y=4(a-x)x=-4(x-
| a |
| 2 |
当
| 2at |
| 1+2t |
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
当
| 2at |
| 1+2t |
| a |
| 2 |
| 1 |
| 2 |
| 2at |
| 1+2t |
则当x=
| 2at |
| 1+2t |
| 8at2 |
| (1+2t)2 |
| 1 |
| 2 |
| a |
| 2 |
当0≤t<
| 1 |
| 2 |
| 2at |
| 1+2t |
| 8at2 |
| (1+2t)2 |

练习册系列答案
相关题目
 内的一个动点,则
内的一个动点,则 的最小值为( ).
的最小值为( ).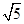


 满足
满足 ,则
,则 的最大值是 .
的最大值是 . (a为常数)所表示的平面区域的面积等于2,则实数a的值为 .
(a为常数)所表示的平面区域的面积等于2,则实数a的值为 .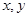 满足约束条件
满足约束条件 则目标函数
则目标函数 的最小值为( )
的最小值为( )