题目内容
设函数f(x)=|x2+2x-1|,若a<b<-1,且f(a)=f(b),则ab+a+b的取值范围为( )
| A.(-∞,-1) | B.(-2,2) | C.(-1,1) | D.(-1,+∞) |
f(x)=|x2+2x-1|=|(x+1)2-2|,图象为对称轴为x=-1抛物线,然后把x轴下方的图形关于x轴翻折上去,
设这个图形与x轴交点分别为x1,x2(x1<x2)
那么在x1<x<x2,f(x)有最大值,在x=-1时取得,f(-1)=2
由f(x)=|x2+2x-1|=2,可得x=-3或者1,
∴-3<a<x1<b<-1,
若a<b<-1且f(a)=f(b),
此时a2+2a-1>0,b2+2b-1<0
那么有a2+2a-1=-(b2+2b-1)
解得:a+b=1-
∴ab+a+b=ab+1-
=1-
.
∵-3<a<b<-1,
∴0<b-a<(-1)-(-3)=2
∴0<(b-a)2<4
∴-1<1-
<1
即:-1<ab+a+b<1
故答案为:(-1,1).
设这个图形与x轴交点分别为x1,x2(x1<x2)
那么在x1<x<x2,f(x)有最大值,在x=-1时取得,f(-1)=2
由f(x)=|x2+2x-1|=2,可得x=-3或者1,
∴-3<a<x1<b<-1,
若a<b<-1且f(a)=f(b),
此时a2+2a-1>0,b2+2b-1<0
那么有a2+2a-1=-(b2+2b-1)
解得:a+b=1-
| a2+b2 |
| 2 |
∴ab+a+b=ab+1-
| a2+b2 |
| 2 |
| (a-b)2 |
| 2 |
∵-3<a<b<-1,
∴0<b-a<(-1)-(-3)=2
∴0<(b-a)2<4
∴-1<1-
| (a-b)2 |
| 2 |
即:-1<ab+a+b<1
故答案为:(-1,1).

练习册系列答案
相关题目

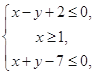 则
则 的取值范围是( )
的取值范围是( ) 

