题目内容
6.化简:2$\sqrt{si{n}^{2}4+co{s}^{2}4-2sin4cos4}$-$\sqrt{2(si{n}^{2}4+si{n}^{2}4)-2(cos4+sin4)(cos4-sin4)}$.
分析 把要求的式子化为2|cos4-sin4|-2|sin4|,在去掉绝对值,可得结果.
解答 解:2$\sqrt{si{n}^{2}4+co{s}^{2}4-2sin4cos4}$-$\sqrt{2(si{n}^{2}4+si{n}^{2}4)-2(cos4+sin4)(cos4-sin4)}$=2|cos4-sin4|-2|sin4|
=2(cos4-sin4)+2sin4=2cos4.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
17.若函数y=x2-3x-4的定义域为[a,b],值域为[-$\frac{25}{4}$,-4].则下列说法正确的是( )
| A. | a=0,b=0 | B. | 若a∈(0,$\frac{3}{2}$),则b∈($\frac{3}{2}$,3) | ||
| C. | 若a=0,则b∈(3,+∞) | D. | 若a∈(0,$\frac{3}{2}$),则b=3 |
14.如果MP,OM分别是角α=$\frac{3π}{16}$的正弦线和余弦线,那么下列结论正确的是( )
| A. | MP<OM<0 | B. | MP<0<OM | C. | MP>OM>0 | D. | OM>MP>0 |
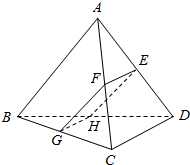 如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.
如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.