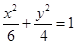题目内容
已知椭圆 :
: 的一个焦点为
的一个焦点为 ,离心率为
,离心率为 .设
.设 是椭圆
是椭圆 长轴上的一个动点,过点
长轴上的一个动点,过点 且斜率为
且斜率为 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)求 的最大值.
的最大值.
 :
: 的一个焦点为
的一个焦点为 ,离心率为
,离心率为 .设
.设 是椭圆
是椭圆 长轴上的一个动点,过点
长轴上的一个动点,过点 且斜率为
且斜率为 的直线
的直线 交椭圆于
交椭圆于 ,
, 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)求
 的最大值.
的最大值.(1) ;(2)
;(2)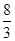 .
.
 ;(2)
;(2)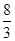 .
.试题分析:(1)由题意,
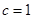 ,
,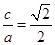 ,根据
,根据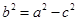 求出
求出 ,则椭圆的方程为
,则椭圆的方程为 . (2)设点
. (2)设点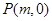 (
(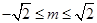 ),则直线
),则直线 的方程为
的方程为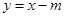 ,联立
,联立 得
得 ,而
,而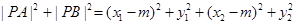
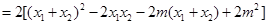 ,带入韦达定理
,带入韦达定理 ,
, ,则
,则
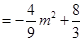 ,而
,而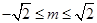 , 即
, 即 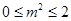 ,则当
,则当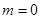 时,
时,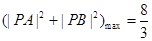 ,
, 的最大值为
的最大值为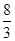 .
.试题解析:(1)由已知,
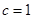 ,
,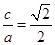 ,
,∴
 ,
,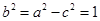 3分
3分∴ 椭圆的方程为
 . 4分
. 4分(2)设点
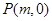 (
(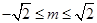 ),则直线
),则直线 的方程为
的方程为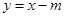 , 2分
, 2分由
 消去
消去 ,得
,得 4分
4分设
 ,
,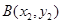 ,则
,则 ,
, 6分
6分∴

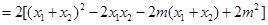
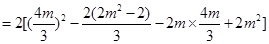
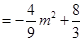 8分
8分∵
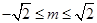 , 即
, 即 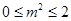
∴当
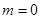 时,
时,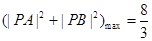 ,
, 的最大值为
的最大值为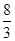 . 10分
. 10分
练习册系列答案
相关题目
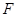 为椭圆
为椭圆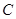
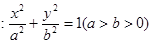 右焦点,圆
右焦点,圆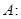
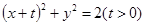 与椭圆
与椭圆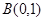 ,且直线
,且直线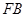 与圆
与圆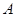 相切于点
相切于点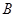 .
.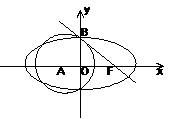
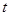 的值及椭圆
的值及椭圆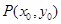 满足
满足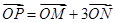 ,其中M、N是椭圆
,其中M、N是椭圆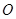 为原点,直线OM与ON的斜率之积为
为原点,直线OM与ON的斜率之积为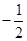 ,求证:
,求证: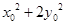 为定值.
为定值. +y2=1的焦点,点A,B在椭圆上,若
+y2=1的焦点,点A,B在椭圆上,若 =5
=5 ;则点A的坐标是 _________ .
;则点A的坐标是 _________ . 上的点到直线
上的点到直线 的最大距离是 .
的最大距离是 . 的左、右焦点,A、B是以O(O
的左、右焦点,A、B是以O(O B.
B. C.
C. D.
D.
 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点 作直线
作直线 的垂线,垂足为
的垂线,垂足为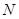 .若
.若 ,其中
,其中 为常数,则动点
为常数,则动点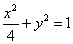 上任意一点P及点
上任意一点P及点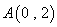 ,则
,则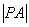 的最大值为
的最大值为  与椭圆
与椭圆 相交于
相交于 、
、 两点,若椭圆的离心率为
两点,若椭圆的离心率为 ,焦距为2,则线段
,焦距为2,则线段 的长是( )
的长是( )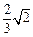



 的右焦点为
的右焦点为 ,椭圆
,椭圆 与
与 轴正半轴交于
轴正半轴交于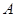 点,与
点,与 轴正半轴交于
轴正半轴交于 ,且
,且 ,则椭圆
,则椭圆