题目内容
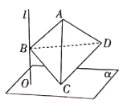
【题目】如图,直线![]() 平面
平面![]() ,垂足为
,垂足为![]() ,三棱锥
,三棱锥![]() 的底面边长和侧棱长都为4,
的底面边长和侧棱长都为4,![]() 在平面
在平面![]() 内,
内,![]() 是直线
是直线![]() 上的动点,则点
上的动点,则点![]() 到平面
到平面![]() 的距离为_______,点
的距离为_______,点![]() 到直线
到直线![]() 的距离的最大值为_______.
的距离的最大值为_______.
【答案】![]()
![]()
【解析】
三棱锥![]() 的底面边长和侧棱长都为4,所以
的底面边长和侧棱长都为4,所以![]() 在平面
在平面![]() 的投影为
的投影为![]() 的重心,利用解直角三角形,即可求出点
的重心,利用解直角三角形,即可求出点![]() 到平面
到平面![]() 的距离;
的距离;![]() ,可得点
,可得点![]() 是以
是以![]() 为直径的球面上的点,所以
为直径的球面上的点,所以![]() 到直线
到直线![]() 的距离为以
的距离为以![]() 为直径的球面上的点到
为直径的球面上的点到![]() 的距离,
的距离,
最大距离为分别过![]() 和
和![]() 的两个平行平面间距离加半径,即可求出结论.
的两个平行平面间距离加半径,即可求出结论.
![]() 边长为
边长为![]() ,则中线长为
,则中线长为![]() ,
,
点![]() 到平面
到平面![]() 的距离为
的距离为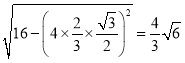 ,
,
点![]() 是以
是以![]() 为直径的球面上的点,
为直径的球面上的点,
所以![]() 到直线
到直线![]() 的距离为以
的距离为以![]() 为直径的球面上的点到
为直径的球面上的点到![]() 的距离,
的距离,
最大距离为分别过![]() 和
和![]() 的两个平行平面间距离加半径.
的两个平行平面间距离加半径.
又三棱锥![]() 的底面边长和侧棱长都为4,
的底面边长和侧棱长都为4,
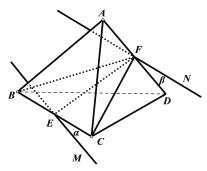
以下求过![]() 和
和![]() 的两个平行平面间距离,
的两个平行平面间距离,
分别取![]() 中点
中点![]() ,连
,连![]() ,
,
则![]() ,同理
,同理![]() ,
,
分别过![]() 做
做![]() ,
,
直线![]() 确定平面
确定平面![]() ,直线
,直线![]() 确定平面
确定平面![]() ,
,
则![]() ,同理
,同理![]() ,
,
![]() 为所求,
为所求,![]() ,
,
![]() ,
,
所以![]() 到直线
到直线![]() 最大距离为
最大距离为![]() .
.
故答案为:![]() ;
;![]() .
.

练习册系列答案
相关题目