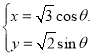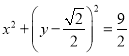题目内容
【题目】已知动圆过定点
，且与直线
相切，动圆圆心的轨迹为
，过
作斜率为
的直线
与交于两点
，过分别作的切线，两切线的交点为
，直线
与交于两点
．
（1）证明：点始终在直线
上且
；
（2）求四边形
的面积的最小值．
【答案】（1）见解析（2）最小值为32．
【解析】
（1）根据抛物线的定义，判断出
的轨迹为抛物线，并由此求得轨迹的方程.设出
两点的坐标，利用导数求得切线
的方程，由此求得
点的坐标.写出直线
的方程，联立直线的方程和曲线的方程，根据韦达定理求得点的坐标，并由此判断出始终在直线
上，且
.
（2）设直线
的倾斜角为
，求得
的表达式，求得
的表达式，由此求得四边形
的面积的表达式进而求得四边形的面积的最小值．
(1)∵动圆过定点
，且与直线
相切，∴动圆圆心到定点和定直线
的距离相等，∴动圆圆心的轨迹是以为焦点的抛物线，∴轨迹的方程为：
，
设
，∴直线
的方程为：
，即：
①，同理，直线
的方程为：
②，
由①②可得：
，
直线方程为：
，联立
可得：
，
，∴点始终在直线上且；
（2）设直线的倾斜角为，由（1）可得：
，
，
∴四边形的面积为：
，当且仅当
或
，即
时取等号，∴四边形的面积的最小值为32.
练习册系列答案
通城学典默写能手系列答案
相关题目
