题目内容
17.(本小题满分8分)如图,正方体ABCD—A1B1C1D1中,E为DD1中点,
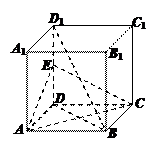 (1)求证:BD1∥平面AEC;
(1)求证:BD1∥平面AEC;
(2)求:异面直线BD与AD1所成的角的大小.
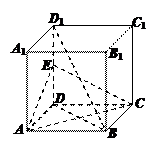 (1)求证:BD1∥平面AEC;
(1)求证:BD1∥平面AEC;(2)求:异面直线BD与AD1所成的角的大小.
证明:(1)设AC、BD交点为O,连结EO,
∵E、O分别是DD1、BD中点
∴EO∥BD1
又∵EO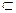 面AEC,BD1
面AEC,BD1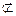 ∥面AEC
∥面AEC
∴BD1∥平面AEC
(2)连结B1D1,AB1
∵DD1 ∥=BB1 ∴B1D1 ∥=BD
∴∠AD1B1即为BD与AD1所成的角
在正方体中有面对角线AD1 = D1B1 = AB1
∴△AD1B1为正三角形
∴∠AD1B1 = 60°
即异面直线BD与AD1所成的角的大小为60°
∵E、O分别是DD1、BD中点
∴EO∥BD1
又∵EO
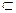 面AEC,BD1
面AEC,BD1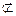 ∥面AEC
∥面AEC∴BD1∥平面AEC
(2)连结B1D1,AB1
∵DD1 ∥=BB1 ∴B1D1 ∥=BD
∴∠AD1B1即为BD与AD1所成的角
在正方体中有面对角线AD1 = D1B1 = AB1
∴△AD1B1为正三角形
∴∠AD1B1 = 60°
即异面直线BD与AD1所成的角的大小为60°
略

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
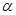 ,
,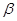 ,
,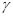 两两互相垂直,点
两两互相垂直,点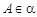 ,点
,点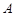 到
到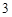 ,点
,点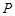 是
是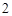 倍,则点
倍,则点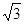
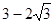
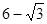
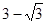
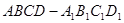 的侧面
的侧面 内有一动点
内有一动点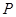 到直线
到直线 与直线
与直线 的距离相等,则动点
的距离相等,则动点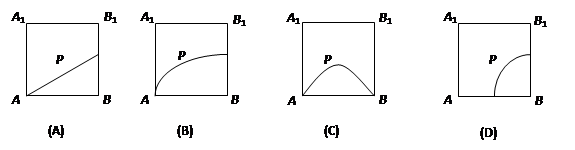
 中,平面
中,平面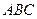 ∥平面
∥平面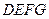 ,
,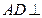 平面
平面 ,
,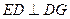 ,
,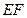 ∥
∥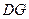 ,且
,且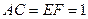 ,
,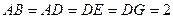 .
.
 平面
平面 ∥平面
∥平面 ;
;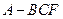 的体积.
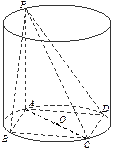
的体积.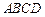 内接于圆柱下底面的圆
内接于圆柱下底面的圆 ,
,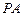 是圆柱的母线,若
是圆柱的母线,若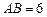 ,
,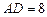 ,此圆柱的体积为
,此圆柱的体积为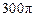 ,求异面直线
,求异面直线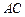 与
与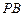 所成角的余弦值.
所成角的余弦值.
 平面
平面 ,底面
,底面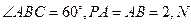 为
为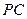 的中点.
的中点. 平面
平面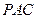 ;
;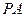 //平面
//平面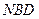 ;
; 的平面角的大小.
的平面角的大小.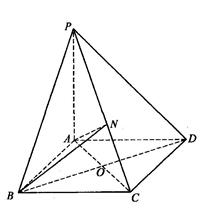
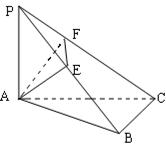
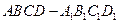 中,异面直线
中,异面直线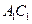 与
与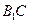 的夹角的大小为__________
的夹角的大小为__________ ,
,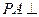 平面
平面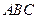 ,
,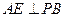 ,
,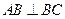 ,
,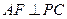 ,
,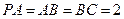 .
.
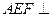 平面
平面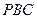 ;
;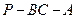 的大小;
的大小;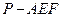 的体
的体 分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于_ __立方分米.
分米,半径是10分米的扇形胶片制作一个圆锥体模型,这个圆锥体的体积等于_ __立方分米.