题目内容
(本小题满分14分)
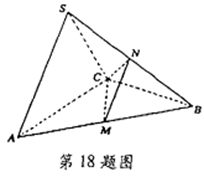
如图所示,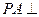 平面
平面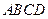 ,底面
,底面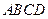 为菱形,
为菱形,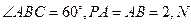 为
为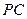 的中点.
的中点.
(1)求证: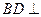 平面
平面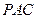 ;
;
(2)求证: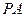 //平面
//平面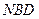 ;
;
(3) 求二面角 的平面角的大小.
的平面角的大小.
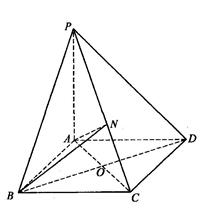
如图所示,
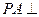 平面
平面 ,底面
,底面 为菱形,
为菱形,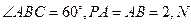 为
为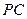 的中点.
的中点.(1)求证:
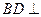 平面
平面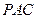 ;
;(2)求证:
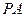 //平面
//平面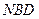 ;
;(3) 求二面角
 的平面角的大小.
的平面角的大小.
解:(1) ………5分
………5分
(2)连结NO,证明PA//NO即可………5分
(3)由(l)可知,BO⊥平面PAC,故在平面PAC内,作OM⊥A,
连结BM(如图),则∠BMO为二面角 的平
的平
面角.在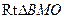 中,易知
中,易知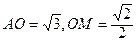
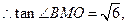
即二面角 的正切值为
的正切值为 …………14分
…………14分
 ………5分
………5分(2)连结NO,证明PA//NO即可………5分
(3)由(l)可知,BO⊥平面PAC,故在平面PAC内,作OM⊥A,
连结BM(如图),则∠BMO为二面角
 的平
的平面角.在
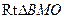 中,易知
中,易知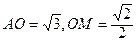
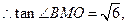
即二面角
 的正切值为
的正切值为 …………14分
…………14分略

练习册系列答案
相关题目
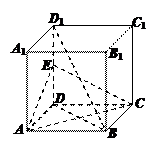 (1)求证:BD1∥平面AEC;
(1)求证:BD1∥平面AEC; ,
,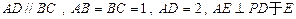 ,
, 。
。
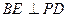 ;
; ;
; ,四棱锥
,四棱锥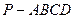 的底面是边长为
的底面是边长为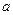 的菱形,
的菱形,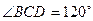 ,
,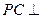 平面
平面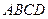 ,
,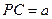 ,
,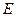 为
为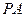 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;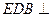 平面
平面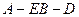 的正切值。
的正切值。
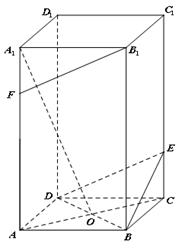
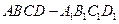 中,底面
中,底面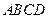 是正方形,侧棱与底面垂直,点
是正方形,侧棱与底面垂直,点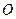 是正方形
是正方形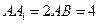 ,点
,点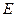 ,
,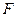 分别在
分别在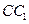 和
和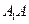 上,且
上,且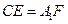 .
.
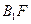 ∥平面
∥平面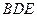 ;
;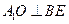 ,求
,求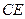 的长;
的长;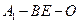 的余弦值.
的余弦值.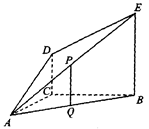
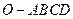 中,底面
中,底面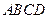 是边长为1的菱形,
是边长为1的菱形,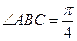 ,
, 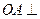 底面
底面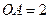 ,
,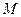 为
为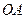 的中点.
的中点.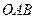 与平面
与平面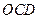 所成的二面角的余弦值.
所成的二面角的余弦值.
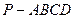 中,若侧棱
中,若侧棱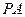 与底面
与底面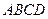 所成的角大小为
所成的角大小为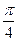 ,则此正四棱锥的斜高长为______________________.
,则此正四棱锥的斜高长为______________________.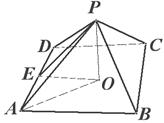
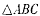 是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,
是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,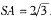 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.