题目内容
空间点到平面的距离如下定义:过空间一点作平面的垂线,该点和垂足之间的距离即为该点到平面的距离.平面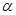 ,
,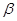 ,
,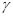 两两互相垂直,点
两两互相垂直,点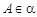 ,点
,点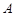 到
到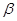 ,
,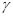 的距离都是
的距离都是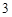 ,点
,点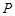 是
是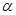 上的动点,满足
上的动点,满足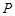 到
到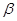 的距离是到
的距离是到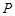 到点
到点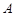 距离的
距离的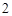 倍,则点
倍,则点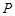 的轨迹上的点到
的轨迹上的点到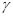 的距离的最小值为
的距离的最小值为
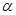 ,
,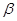 ,
,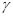 两两互相垂直,点
两两互相垂直,点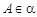 ,点
,点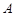 到
到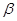 ,
,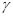 的距离都是
的距离都是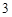 ,点
,点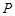 是
是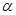 上的动点,满足
上的动点,满足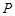 到
到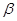 的距离是到
的距离是到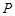 到点
到点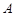 距离的
距离的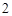 倍,则点
倍,则点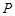 的轨迹上的点到
的轨迹上的点到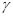 的距离的最小值为
的距离的最小值为A.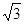 | B.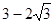 |
C.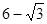 | D.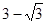 |
D
原题等价于在直角坐标系中,点A(3,3),P第一象限内的动点,满足P到Y轴的距离是到P到点A 距离的2倍,则点P的轨迹上的点到x轴的距离的最小值是多少.
解:设P(x,y),
P的轨迹方程为x=2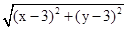 ,
,
x2=4(x-3)2+4(y-3)2,
(y-3)2=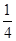 [x2-4(x-3)2]-
[x2-4(x-3)2]-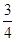 x2+6x-9,
x2+6x-9,
当x=4时,最大值为3
∵(y-3)2=3,∴y=3+ ,或y=3-
,或y=3-
∴点P 的轨迹上的点到γ 的距离的最小值是3-
故选D.
解:设P(x,y),
P的轨迹方程为x=2
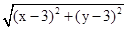 ,
,x2=4(x-3)2+4(y-3)2,
(y-3)2=
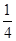 [x2-4(x-3)2]-
[x2-4(x-3)2]-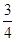 x2+6x-9,
x2+6x-9,当x=4时,最大值为3
∵(y-3)2=3,∴y=3+
 ,或y=3-
,或y=3-
∴点P 的轨迹上的点到γ 的距离的最小值是3-

故选D.

练习册系列答案
相关题目
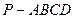 的底面
的底面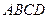 是正方形,侧棱
是正方形,侧棱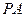
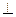 底面
底面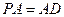 ,
,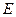 、
、 分别是棱
分别是棱 、
、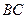 的中点.
的中点. 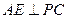 ; (2) 求直线
; (2) 求直线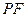 与平面
与平面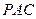 所成的角的正切值
所成的角的正切值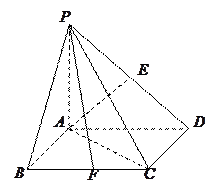
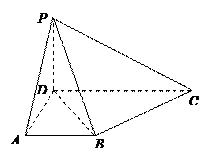
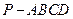 中,侧面
中,侧面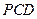
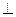 底面
底面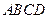 ,
,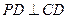 ,底面
,底面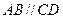 ,
,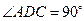 ,
,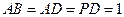 ,
,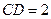 .
.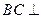 平面
平面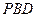 ;
;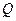 为侧棱
为侧棱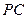 上一点,
上一点,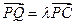 ,
,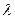 的值,使得二面角
的值,使得二面角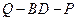 为
为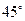 .
.
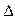 ABC的边长为1,AE
ABC的边长为1,AE 平面ABC,CD∥AE,且CD=
平面ABC,CD∥AE,且CD=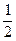 AE.
AE.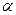 ,AE=
,AE=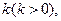 若
若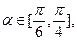 求
求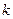 的取值范围;
的取值范围;
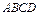 所在的平面与平面
所在的平面与平面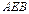 垂直,且
垂直,且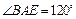 ,
,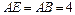 ,
,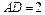 ,
,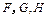 分别为
分别为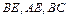 的中点.
的中点.
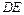 与平面
与平面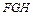 平行;
平行;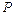 在直线
在直线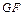 上,且二面角
上,且二面角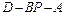 的大小为
的大小为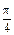 ,试确定点
,试确定点 面ABC,AB
面ABC,AB
 面PAB的距
面PAB的距 离.
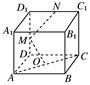
离.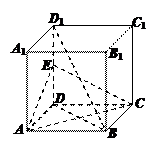 (1)求证:BD1∥平面AEC;
(1)求证:BD1∥平面AEC;