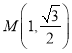Question

【题目】已知函数f（x）＝xlnx，函数g（x）＝kx﹣cosx在点处的切线平行于x轴.

（1）求函数f（x）的极值；

（2）讨论函数F（x）＝g（x）﹣f（x）的零点的个数.

Answer 1

【答案】（1）极小值为f（），无极大值（2）F（x）有且仅有2个零点

【解析】

（1）利用函数f（x）的导数判断函数的单调性，然后求出函数的极值；

（2）因为F（x）＝x﹣cosx﹣xlnx，F'（x）＝sinx﹣lnx，设h（x）＝sinx﹣lnx，分类讨论：（i）当x∈（e，+∞）时，h（x）＝F'（x）≤0，则F（x）单调递减，此时可得F（x）在（e，）上存在唯一零点，也即在（e，+∞）上存在唯一零点；（ii）当x∈（，e]时，，则F'（x）在（，e]单调递减，此时F（x）在（，e]上恒大于0，无零点；（iii）当x∈（0，1）时，，所以在（0，1）上单调递减，此时F（x）在（，]上存在唯一零点，即F（x）在（0，]上存在唯一零点

解：（1）因为函数f（x）＝xlnx的定义域为（0，+∞），

所以，

令，即lnx+1＜0，解得0＜x，

所以f（x）的单调递减区间为（0，），

令，即lnx+1＞0，解得，

所以f（x）的单调递增区间为（，+∞），

综上，f（x）的极小值为f（），无极大值；

（2）由，得）＝k﹣1＝0，故k＝1，所以g（x）＝x﹣cosx，

因为F（x）＝x﹣cosx﹣xlnx，，

设h（x）＝sinx﹣lnx，

（i）当x∈（e，+∞）时，，则单调递减，

又F（e）＝﹣cose＞0， ，

故F（x）在（e，）上存在唯一零点，也即在（e，+∞）上存在唯一零点；

（ii）当x∈（，e]时， ，则在单调递减，

因为，

所以存在，使得，且在上，在（x0，e]上，

所以为F（x）在（，e]上的最大值，

又因为F（e）＝﹣cose＞0，F（）（1﹣ln）＞0，

所以F（x）在（，e]上恒大于0，无零点；

（iii）当x∈（0，1）时，，

所以在（0，1）上单调递减，

当x∈[1，]时，，

设t（x）＝xcosx﹣1，所以，

所以t（x）在[1，]上单调递减，

所以t（x）＜t（1）＝cos1﹣1＜0，即，

所以在（0，]上单调递减，

因为，所以F（x）在上单调递增，

因为F（）（1﹣ln）＞0，

，

所以F（x）在（，]上存在唯一零点，即F（x）在（0，]上存在唯一零点，

综上，F（x）有且仅有2个零点