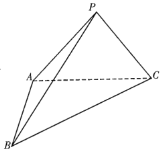
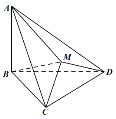
题目内容
【题目】已知
，
，
分别为
的中点，
，将
沿
折起，得到四棱锥
，
为
的中点.
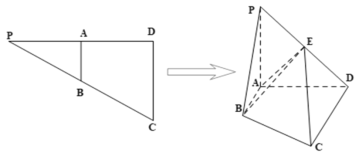
（1）证明：
平面
；
（2）当正视图方向与向量
的方向相同时，此时的正视图的面积为
，求四棱锥的体积.
【答案】（1）证明见解析；（2）
【解析】
（1）根据题意可知
，由三线合一可证明
，进而由线面垂直的判定可证明
平面
；
（2）根据平面
平面
，所以
在平面
内的射影应该落在直线
上，所以点到平面的距离为
，进一步求出点到平面的距离，然后代入锥体体积公式计算即可.
解：（1）由平面图可知，
，
，
，
所以
平面，所以.
因为
为
的中点，
，∴.
因为
，所以平面.
（2）因为
的正视图与
全等，所以
，
∴
，∴
或
.
由（1）可知，平面平面，所以在平面内的射影应该落在直线
上，所以点到平面的距离为，
所以四棱锥的体积
.
练习册系列答案
名校课堂系列答案
相关题目
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一，为坚决打赢脱贫攻坚战，某帮扶单位考察了甲乙两种不同的农产品加工生产方式，现对两种生产方式加工的产品质量进行测试并打分对比，得到如下数据：
生产方式甲 | 分值区间 |
|
|
|
|
|
频数 | 20 | 30 | 100 | 40 | 10 | |
生产方式乙 | 分值区间 |
|
|
|
|
|
频数 | 25 | 35 | 60 | 50 | 30 |
其中产品质量按测试指标可划分为：指标在区间
上的为特优品，指标在区间
上的为一等品，指标在区间
上的为二等品．
（1）用事件
表示“按照生产方式甲生产的产品为特优品”，估计的概率；
（2）填写下面列联表，并根据列联表判断能否有
的把握认为“特优品”与生产方式有关？
特优品 | 非特优品 | |
生产方式甲 | ||
生产方式乙 |
（3）根据打分结果对甲乙两种生产方式进行优劣比较．
附表：
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式：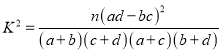
，其中
．
