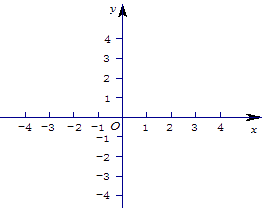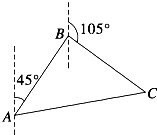题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() ,
, ![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() 恰为数列
恰为数列![]() 中的一项?若存在,求所有满足要求的
中的一项?若存在,求所有满足要求的![]() ;若不存在,说明理由.
;若不存在,说明理由.
【答案】(1)![]() ,
, ![]() (2)满足要求的
(2)满足要求的![]() 为
为![]() ,
, ![]() .
.
【解析】试题分析:(1)由和项与通项关系得![]() ,根据等比数列定义及通项公式可得
,根据等比数列定义及通项公式可得![]() ,由叠乘法可得
,由叠乘法可得![]() ,再由和项与通项关系得
,再由和项与通项关系得![]() ,根据等差数列定义及通项公式可得
,根据等差数列定义及通项公式可得![]() (2)先研究数列
(2)先研究数列![]() 增减性:
增减性: ![]() ,再研究确定可能情况:2,3,7,即得满足要求的
,再研究确定可能情况:2,3,7,即得满足要求的![]()
试题解析:解:(1)因为![]() ,所以当
,所以当![]() 时,
时, ![]() ,
,
两式相减得![]() ,即
,即![]() ,又
,又![]() ,则
,则![]() ,
,
所以数列![]() 是以
是以![]() 为首项,2为公比的等比数列,故
为首项,2为公比的等比数列,故![]() .
.
由![]() 得
得![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() ,
,
以上![]() 个式子相乘得
个式子相乘得![]() ,即
,即![]() ①,当
①,当![]() 时,
时, ![]() ②,
②,
两式相减得![]() ,即
,即![]() (
(![]() ),
),
所以数列![]() 的奇数项、偶数项分别成等差数列,
的奇数项、偶数项分别成等差数列,
又![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以数列![]() 是以
是以![]() 为首项,1为公差的等差数列,因此数列
为首项,1为公差的等差数列,因此数列![]() 的通项公式为
的通项公式为![]()
(2)当![]() 时,
时, ![]() 无意义,
无意义,
设![]() (
(![]() ,
, ![]() ),显然
),显然![]() .
.
则![]()
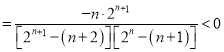 ,即
,即![]() .
.
显然![]() ,所以
,所以![]() ,
,
所以存在![]() ,使得
,使得![]() ,
, ![]() ,
,
下面证明不存在![]() ,否则
,否则![]() ,即
,即![]() ,
,
此式右边为3的倍数,而![]() 不可能是3的倍数,故该式不成立.
不可能是3的倍数,故该式不成立.
综上,满足要求的![]() 为
为![]() ,
, ![]() .
.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】2016年入冬以来,各地雾霾天气频发, ![]() 频频爆表(
频频爆表(![]() 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与![]() 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与![]() 的数据如下表:
的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
(1)请根据上述数据,在下面给出的坐标系中画出散点图;
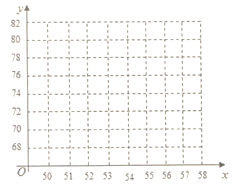
(2)试判断![]() 与
与![]() 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,若没有,请说明理由;
,若没有,请说明理由;
(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的![]() 的浓度(保留整数).
的浓度(保留整数).
参考公式: 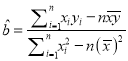
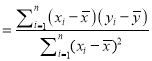 ,
, ![]() .
.