جâؤ؟ؤعبف
،¾جâؤ؟،؟تـح»بçئنہ´µؤذآ¹عزكاéµؤس°دى£¬ب«¹ْ¸÷µطر§ذ£¶¼حئ³ظ2020ؤêµؤ´؛¼¾؟ھر§.ؤ³ر§ذ£،°ح£؟خ²»ح£ر§،±£¬ہûسأشئ؟خئ½ج¨جل¹©أâ·ردكةد؟خ³ج.¸أر§ذ£خھءث½âر§ةْ¶شدكةد؟خ³جµؤآْزâ³ج¶ب£¬ثو»ْ³éب،ءث500أûر§ةْ¶ش¸أدكةد؟خ³جئہ·ض.ئنئµآت·ض²¼ض±·½ح¼بçدآ£؛بô¸ù¾فئµآت·ض²¼ض±·½ح¼µأµ½µؤئہ·ضµحسع80·ضµؤ¸إآت¹ہ¼ئضµخھ0.45.
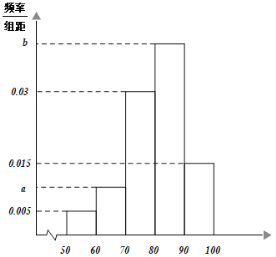
£¨1£©£¨i£©اَض±·½ح¼ضذµؤa£¬bضµ£»
£¨ii£©بôئہ·ضµؤئ½¾ùضµ؛حضعت¾ù²»µحسع80·ضتسخھآْز⣬إذ¶د¸أذ£ر§ةْ¶شدكةد؟خ³جتا·ٌآْزâ£؟²¢ثµأ÷ہيسة£¨ح¬ز»×éضذµؤت¾فسأ¸أ×éاّ¼نµؤضذµمضµخھ´ْ±ي£©£»
£¨2£©بô²ةسأ·ض²م³éرùµؤ·½·¨£¬´سرù±¾ئہ·ضشع[60£¬70£©؛ح[90£¬100]ؤعµؤر§ةْضذ¹²³éب،5بث½ّذذ²âتشہ´¼ىرéثûأاµؤحّ؟خر§د°ذ§¹û£¬شظ´سضذر،ب،2بث½ّذذ¸ْ×ظ·ضخِ£¬اَصâ2بثضذضءةظز»بثئہ·ضشع[60£¬70£©ؤعµؤ¸إآت.
،¾´ً°¸،؟£¨1£©£¨i£©a£½0.01£»b£½0.04£¨ii£©¸أذ£ر§ةْ¶شدكةد؟خ³جآْز⣬دê¼û½âخِ£¨2£©![]()
،¾½âخِ،؟
£¨1£©![]() سةئµآت·ض²¼ض±·½ح¼ضذذ،¾طذخأو»ض®؛حخھ1£¬ؤـاَ³ِ
سةئµآت·ض²¼ض±·½ح¼ضذذ،¾طذخأو»ض®؛حخھ1£¬ؤـاَ³ِ![]() £¬
£¬![]() £®
£®
![]() سةئµآت·ض²¼ض±·½ح¼ؤـاَ³ِئہ·ضµؤضعت؛حئہ·ضµؤئ½¾ùضµ£¬´س¶ّµأµ½¸أذ£ر§ةْ¶شدكةد؟خ³جآْز⣮
سةئµآت·ض²¼ض±·½ح¼ؤـاَ³ِئہ·ضµؤضعت؛حئہ·ضµؤئ½¾ùضµ£¬´س¶ّµأµ½¸أذ£ر§ةْ¶شدكةد؟خ³جآْز⣮
£¨2£©سةجâضھئہ·ضشع![]() £¬
£¬![]() ؛ح
؛ح![]() £¬
£¬![]() ؤعµؤئµآت·ض±ًخھ0.1؛ح0.15£¬شٍ³éب،µؤ5بثضذ£¬ئہ·ضشع
ؤعµؤئµآت·ض±ًخھ0.1؛ح0.15£¬شٍ³éب،µؤ5بثضذ£¬ئہ·ضشع![]() £¬
£¬![]() ؤعµؤخھ2بث£¬ئہ·ضشع
ؤعµؤخھ2بث£¬ئہ·ضشع![]() £¬
£¬![]() µؤسذ3بث£¬¼ائہ·ضشع
µؤسذ3بث£¬¼ائہ·ضشع![]() £¬
£¬![]() ؤعµؤ3خ»ر§ةْخھ
ؤعµؤ3خ»ر§ةْخھ![]() £¬
£¬![]() £¬
£¬![]() £¬ئہ·ضشع
£¬ئہ·ضشع![]() £¬
£¬![]() ؤعµؤ2خ»ر§ةْصâ
ؤعµؤ2خ»ر§ةْصâ![]() £¬
£¬![]() £¬´س5بثضذبخر،2بث£¬ہûسأءذ¾ظ·¨ؤـاَ³ِصâ2بثضذضءةظز»بثئہ·ضشع
£¬´س5بثضذبخر،2بث£¬ہûسأءذ¾ظ·¨ؤـاَ³ِصâ2بثضذضءةظز»بثئہ·ضشع![]() £¬
£¬![]() µؤ¸إآت£®
µؤ¸إآت£®
½â£؛£¨1£©![]() سةزرضھµأ
سةزرضھµأ![]() £¬
£¬
½âµأ![]() £¬
£¬
سض![]() £¬
£¬![]() £®
£®
![]() سةئµآت·ض²¼ض±·½ح¼µأئہ·ضµؤضعتخھ85£¬
سةئµآت·ض²¼ض±·½ح¼µأئہ·ضµؤضعتخھ85£¬
ئہ·ضµؤئ½¾ùضµخھ![]() £¬
£¬
![]() ¸أذ£ر§ةْ¶شدكةد؟خ³جآْز⣮
¸أذ£ر§ةْ¶شدكةد؟خ³جآْز⣮
£¨2£©سةجâضھئہ·ضشع![]() £¬
£¬![]() ؛ح
؛ح![]() £¬
£¬![]() ؤعµؤئµآت·ض±ًخھ0.1؛ح0.15£¬
ؤعµؤئµآت·ض±ًخھ0.1؛ح0.15£¬
شٍ³éب،µؤ5بثضذ£¬ئہ·ضشع![]() £¬
£¬![]() ؤعµؤخھ2بث£¬ئہ·ضشع
ؤعµؤخھ2بث£¬ئہ·ضشع![]() £¬
£¬![]() µؤسذ3بث£¬
µؤسذ3بث£¬
¼ائہ·ضشع![]() £¬
£¬![]() ؤعµؤ3خ»ر§ةْخھ
ؤعµؤ3خ»ر§ةْخھ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
ئہ·ضشع![]() £¬
£¬![]() ؤعµؤ2خ»ر§ةْصâ
ؤعµؤ2خ»ر§ةْصâ![]() £¬
£¬![]() £¬
£¬
شٍ´س5بثضذبخر،2بثµؤثùسذ؟ةؤـ½ل¹ûخھ£؛
![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬¹²10ضض£¬
£¬¹²10ضض£¬
ئنضذ£¬ئہ·ضشع![]() £¬
£¬![]() ؤعµؤ؟ةؤـ½ل¹ûخھ
ؤعµؤ؟ةؤـ½ل¹ûخھ![]() £¬
£¬![]() £¬
£¬![]() £¬¹²3ضض£¬
£¬¹²3ضض£¬
![]() صâ2بثضذضءةظز»بثئہ·ضشع
صâ2بثضذضءةظز»بثئہ·ضشع![]() £¬
£¬![]() µؤ¸إآتخھ
µؤ¸إآتخھ![]() £®
£®