题目内容
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)经过点(﹣2,0)和
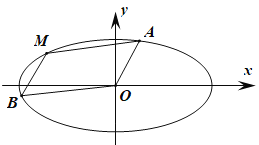
(a>b>0)经过点(﹣2,0)和![]() ,椭圆C上三点A,M,B与原点O构成一个平行四边形AMBO.
,椭圆C上三点A,M,B与原点O构成一个平行四边形AMBO.
(1)求椭圆C的方程;
(2)若点B是椭圆C左顶点,求点M的坐标;
(3)若A,M,B,O四点共圆,求直线AB的斜率.
【答案】(1)![]() +y2=1;(2)M(-1,±
+y2=1;(2)M(-1,±![]() );(3)±
);(3)±![]()
【解析】
(1)将点![]() 和
和![]() 代入椭圆
代入椭圆![]() +
+![]() =1求解即可.
=1求解即可.
(2)根据平行四边形AMBO可知AM∥BO,且AM=BO=2.再设点M(x0,y0),则A(x0+2,y0),代入椭圆C求解即可.
(3) 因为A,M,B,O四点共圆,所以平行四边形AMBO是矩形,且OA⊥OB,再联立直线与椭圆的方程,结合韦达定理代入![]() ·
·![]() =x1x2+y1y2=0求解即可.
=x1x2+y1y2=0求解即可.
(1)因为椭圆![]() +
+![]() =1(a>b>0)过点
=1(a>b>0)过点![]() 和
和![]() ,
,
所以a=2,![]() +
+![]() =1,解得b2=1,所以椭圆C的方程为
=1,解得b2=1,所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)因为B为左顶点,所以B (-2,0).
因为四边形AMBO为平行四边形,所以AM∥BO,且AM=BO=2.
设点M(x0,y0),则A(x0+2,y0).
因为点M,A在椭圆C上,所以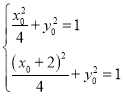 解得
解得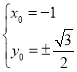 所以M(-1,±
所以M(-1,±![]() ).
).
(3)因为直线AB的斜率存在,所以设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2).
由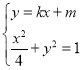 消去y,得(4k2+1)x2+8kmx+4m2-4=0,
消去y,得(4k2+1)x2+8kmx+4m2-4=0,
则有x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
因为平行四边形AMBO,所以![]() =
=![]() +
+![]() =(x1+x2,y1+y2).
=(x1+x2,y1+y2).
因为x1+x2=![]() ,所以y1+y2=k(x1+x2)+2m=k·
,所以y1+y2=k(x1+x2)+2m=k·![]() +2m=
+2m=![]() ,所以M(
,所以M(![]() ,
,![]() ).
).
因为点M在椭圆C上,所以将点M的坐标代入椭圆C的方程,化得4m2=4k2+1.①
因为A,M,B,O四点共圆,所以平行四边形AMBO是矩形,且OA⊥OB,
所以![]() ·
·![]() =x1x2+y1y2=0.
=x1x2+y1y2=0.
因为y1y2=(kx1+m)(kx1+m)=k2x1x2+km(x1+x2)+m2=![]() ,
,
所以x1x2+y1y2=![]() +
+![]() =0,化得5m2=4k2+4.②
=0,化得5m2=4k2+4.②
由①②解得k2=![]() ,m2=3,此时△>0,因此k=±
,m2=3,此时△>0,因此k=±![]() .
.
所以所求直线AB的斜率为±![]() .
.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案