题目内容
5．用平面在正方体上截下一个三棱锥，以原来正方体的那个顶点作为三棱锥的顶点，则该顶点在三棱锥的底面上的射影是这个三角形的（ ）| A． | 重心 | B． | 外心 | C． | 内心 | D． | 垂心 |
分析 一条侧棱就垂直于另外两条侧棱所组成的面，即垂直于在面上的底面的一条边，过顶点向底面做垂线，连接底面的顶点和垂足，根据三垂线定理得到连线是高线，得到三条高线的交点是垂心．
解答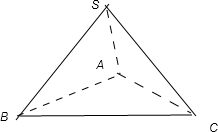 
解：用平面在正方体上截下一个三棱锥，以原来正方形的那个顶点作为三棱锥的顶点，
则三棱锥的三条侧棱中，每两条之间的夹角都是90°，
则三条侧棱两两垂直，
即SB⊥SA，SB⊥SC，
∵SA∩SC=S，
∴SB⊥面SAC，
∵AC?面SAC，
∴SB⊥AC，
过S向底面做垂线，垂足为O，连接BO，并延长交AC于D，
由三垂线定理知BD⊥AC，即BD 是三角形的高线，
∴三棱锥的顶点在底面的射影是底面三角形的垂心，
故选：D
点评 本题考查棱锥的结构特征，考查逻辑思维能力和空间思维能力，是基础题．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
16．已知椭圆C1，抛物线C2的焦点均在x轴上，从两条曲线上各取两个点，将其坐标混合记录于下表中：
（1）求椭圆C1和抛物线C2的标准方程．
（2）过椭圆C1右焦点F的直线l与此椭圆相交于A，B两点，若点P为直线x=4上任意一点，试证：直线PA，PF，PB的斜率成等差数列．
| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
（2）过椭圆C1右焦点F的直线l与此椭圆相交于A，B两点，若点P为直线x=4上任意一点，试证：直线PA，PF，PB的斜率成等差数列．
13．
如图，某大风车的半径为2m，每6s旋转一周，它的最低点O离地面0.5 m．风车圆周上一点A从最低点O开始，运动t（s）后与地面的距离为h（m），则函数h=f（t）的关系式（ ）
如图，某大风车的半径为2m，每6s旋转一周，它的最低点O离地面0.5 m．风车圆周上一点A从最低点O开始，运动t（s）后与地面的距离为h（m），则函数h=f（t）的关系式（ ）| A． | y=-2cos$\frac{πt}{6}$+2.5 | B． | y=-2sin$\frac{πt}{6}$+2.5 | C． | y=-2cos$\frac{πt}{3}$+2.5 | D． | y=-2sin$\frac{πt}{3}$+2.5 |
17．“五一”期间，三个家庭（每家均为一对夫妇和一个孩子）去“抚顺三块石国家森林公园”游玩，在某一景区前合影留念，要求前排站三个小孩，后排为三对夫妇，则每队夫妇均相邻，且小孩恰与自家父母排列的顺序一致的概率（ ）
| A． | $\frac{1}{15}$ | B． | $\frac{1}{90}$ | C． | $\frac{1}{180}$ | D． | $\frac{1}{360}$ |
14．已知$\overrightarrow{e}$和$\overrightarrow{f}$是互相垂直的单位向量，向量$\overrightarrow{{a}_{n}}$满足：$\overrightarrow{e}•\overrightarrow{{a}_{n}}$=n，$\overrightarrow{f}•\overrightarrow{{a}_{n}}$=2n，n∈N*．设θn为$\overrightarrow{{a}_{n+1}}$-$\overrightarrow{{a}_{n}}$和$\overrightarrow{{a}_{n+2}}$-$\overrightarrow{{a}_{n+1}}$的夹角，则（ ）
| A． | On随着n的增大而增大 | B． | On随着n的增大而减小 | ||
| C． | 随着n的增大，On先增大后减小 | D． | 随着n的增大，On先减小后增大 |
15．能化为普通方程x2+y-1=0的参数方程是（ ）
| A． | $\left\{\begin{array}{l}x=sint\\ y={cos^2}t\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=tanφ\\ y=1-{tan^2}φ\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}x=\sqrt{1-t}\\ y=t\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=cosθ}\\{y=si{n}^{2}θ}\end{array}\right.$ |