题目内容
如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形.(1)求抛物线的方程;
(2)过点F的直线交抛物线于A,B两点,交直线l于点M,交y轴于G.
①若
 ,
, ,求证:λ1+λ2为常数;
,求证:λ1+λ2为常数;②求
 的取值范围.
的取值范围.
【答案】分析:(1)利用抛物线的定义求出△PQF的边长为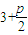 ,写出有关点的坐标,利用两点距离的公式得到|FQ|,列出方程求出p的值,得到抛物线的方程.
,写出有关点的坐标,利用两点距离的公式得到|FQ|,列出方程求出p的值,得到抛物线的方程.
(2)①设出直线的方程,求出M,G的坐标,将已知条件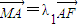 ,
,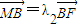 用坐标表示,求出λ1+λ2为常数.
用坐标表示,求出λ1+λ2为常数.
②将直线方程与抛物线方程联立,利用韦达定理得到A,B的坐标和与积,;利用向量的数量积公式表示出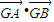 ,将韦达定理得到值代入,求出其范围.
,将韦达定理得到值代入,求出其范围.
解答:解:(1)据题意知,P(3,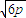 ),△PQF为等边三角形,其边长为
),△PQF为等边三角形,其边长为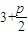 ,Q(
,Q(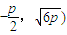 ,
,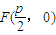
所以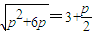 ,解得p=2
,解得p=2
所以抛物线的方程y2=4x
(2)①设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-1)
所以 ;
; 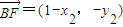
M(-1,-3k),G(0,-k)
所以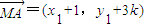 ;
;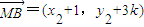
因为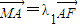 ;
;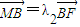
所以λ1=λ2=1,所以λ1+λ2=2
②由 得k2x2-(2k2+4)x+k2=0
得k2x2-(2k2+4)x+k2=0
△=16k2+16>0
所以 ,x1•x2=1,
,x1•x2=1,
y1•y2=k(x1-1)•k(x2-1)=-4;y1+y2=k(x1-1)+k(x2-1)=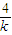
所以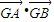 =
=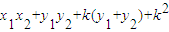
=k2+1≥1
所以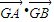 的取值范围为[1,+∞)
的取值范围为[1,+∞)
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合把握所学知识和基本的运算能力.
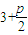 ,写出有关点的坐标,利用两点距离的公式得到|FQ|,列出方程求出p的值,得到抛物线的方程.
,写出有关点的坐标,利用两点距离的公式得到|FQ|,列出方程求出p的值,得到抛物线的方程.(2)①设出直线的方程,求出M,G的坐标,将已知条件
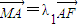 ,
,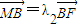 用坐标表示,求出λ1+λ2为常数.
用坐标表示,求出λ1+λ2为常数.②将直线方程与抛物线方程联立,利用韦达定理得到A,B的坐标和与积,;利用向量的数量积公式表示出
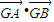 ,将韦达定理得到值代入,求出其范围.
,将韦达定理得到值代入,求出其范围.解答:解:(1)据题意知,P(3,
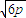 ),△PQF为等边三角形,其边长为
),△PQF为等边三角形,其边长为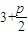 ,Q(
,Q(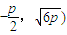 ,
,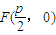
所以
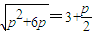 ,解得p=2
,解得p=2所以抛物线的方程y2=4x
(2)①设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x-1)
所以
 ;
; 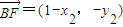
M(-1,-3k),G(0,-k)
所以
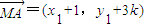 ;
;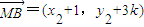
因为
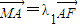 ;
;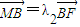
所以λ1=λ2=1,所以λ1+λ2=2
②由
 得k2x2-(2k2+4)x+k2=0
得k2x2-(2k2+4)x+k2=0△=16k2+16>0
所以
 ,x1•x2=1,
,x1•x2=1,y1•y2=k(x1-1)•k(x2-1)=-4;y1+y2=k(x1-1)+k(x2-1)=
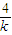
所以
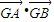 =
=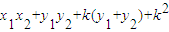
=k2+1≥1
所以
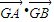 的取值范围为[1,+∞)
的取值范围为[1,+∞)点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合把握所学知识和基本的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
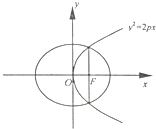 如图,已知抛物线y2=2px(p>0)的焦点恰好是椭圆
如图,已知抛物线y2=2px(p>0)的焦点恰好是椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、2(
| ||||
C、
| ||||
D、
|
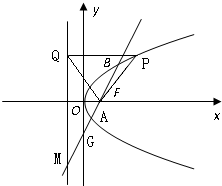 如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形.
如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形. 过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1.
过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1. (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,…. 如图,已知抛物线y2=2px(p>0),过它的焦点F的直线l与其相交于A,B两点,O为坐标原点.
如图,已知抛物线y2=2px(p>0),过它的焦点F的直线l与其相交于A,B两点,O为坐标原点.