题目内容
 过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1.
过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1.(1)求出抛物线的通径,证明x1x2和y1y2都是定值,并求出这个定值;
(2)证明:A1F⊥B1F.
分析:(1)当AB⊥x时,根据抛物线方程得到A、B两点的坐标,直接计算可得通径的长,并且x1x2=
、y1y2=-p2,是定值;当AB与x轴不垂直时,设AB方程的点斜式形式,并且与抛物线联解消去x得到关于y的方程,利用根与系数的关系算出y1y2=-p2,结合抛物线方程即可得到x1x2=
,从而使命题得到证明.
(2)根据题意,得出A1、B1的坐标,从而得到向量
、
的坐标,计算
、
数量积并进行化简得到0,由此即可得到A1F⊥B1F.
| p2 |
| 4 |
| p2 |
| 4 |
(2)根据题意,得出A1、B1的坐标,从而得到向量
| FA1 |
| FB1 |
| FA1 |
| FB1 |
解答:解:∵抛物线方程是y2=2px,
∴抛物线的焦点F(
,0),准线x=-
(1)①当AB⊥x时,可得A(
,p)、B(
,-p),
∴通径长为p-(-p)=2p,
可得此时x1x2=
且y1y2=-p2,是定值.
②AB与x轴不垂直时,设AB:y=k(x-
)(k≠0)
由
消去x,得
y2-y-
=0,
由根与系数的关系,得y1y2=-p2,
再代入到抛物线方程,可得x1x2=
×
=
,是定值.
综上所述,过焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,必有x1x2=
、y1y2=-p2是定值;
(2)根据题意,可得A1(-
,y1)、B1(-
,y2),F(
,0)
∵焦点F(
,0),
∴
=(p,y1),
=(p,y2),
由此可得
•
=p2+y1y2=p2+(-p2)=0,
∴
⊥
,即A1F⊥B1F.
∴抛物线的焦点F(
| p |
| 2 |
| p |
| 2 |
(1)①当AB⊥x时,可得A(
| p |
| 2 |
| p |
| 2 |
∴通径长为p-(-p)=2p,
可得此时x1x2=
| p2 |
| 4 |
②AB与x轴不垂直时,设AB:y=k(x-
| p |
| 2 |
由
|
| k |
| 2p |
| kp |
| 2 |
由根与系数的关系,得y1y2=-p2,
再代入到抛物线方程,可得x1x2=
| y12 |
| 2p |
| y22 |
| 2p |
| p2 |
| 4 |
综上所述,过焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,必有x1x2=
| p2 |
| 4 |
(2)根据题意,可得A1(-
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
∵焦点F(
| p |
| 2 |
∴
| FA1 |
| FB1 |
由此可得
| FA1 |
| FB1 |
∴
| FA1 |
| FB1 |
点评:本题给出抛物线经过焦点的弦的端点A(x1,y1)、B(x2,y2),它们在准线上的射影点分别为A1、B1,求证x1x2和y1y2都是定值并证明A1F⊥B1F.着重考查了抛物线的标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

 的焦点为
的焦点为 ,过
,过 轴的直线与抛物线交于
轴的直线与抛物线交于 两点,已知
两点,已知 .
. 的方程;
的方程; ,过点
,过点 作方向向量为
作方向向量为 的直线与抛物线
的直线与抛物线 两点,求使
两点,求使 为钝角时实数
为钝角时实数 的取值范围;
的取值范围;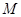
 ,过
,过 为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由。
为直径的圆始终相切?若存在,请求出这条直线;若不存在,请说明理由。 ,过
,过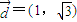 的直线与抛物线C相交于A,B两点,求使∠AFB为钝角时实数m的取值范围;
的直线与抛物线C相交于A,B两点,求使∠AFB为钝角时实数m的取值范围;