题目内容
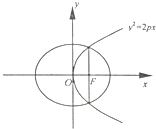 如图,已知抛物线y2=2px(p>0)的焦点恰好是椭圆
如图,已知抛物线y2=2px(p>0)的焦点恰好是椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、2(
| ||||
C、
| ||||
D、
|
分析:先求出抛物线y2=2px(p>0)的焦点坐标,再利用两条曲线的交点的连线过F,求出其中一个交点的坐标,最后利用定义求出2a和2c就可求得椭圆的离心率.
解答: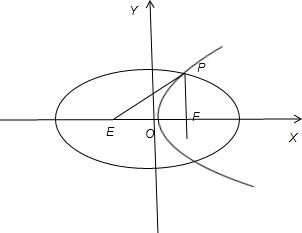 解:因为抛物线y2=2px(p>0)的焦点F为(
解:因为抛物线y2=2px(p>0)的焦点F为(
,0),设椭圆另一焦点为E.
当x=
时代入抛物线方程得y=±p.又因为PQ经过焦点F,所以P(
,p)且PF⊥OF.
所以|PE|=
=
p,|PF|=P.|EF|=p.
故2a=
p+p,2c=p.e=
=
-1.
故选 A.
 解:因为抛物线y2=2px(p>0)的焦点F为(
解:因为抛物线y2=2px(p>0)的焦点F为(| p |
| 2 |
当x=
| p |
| 2 |
| p |
| 2 |
所以|PE|=
(
|
| 2 |
故2a=
| 2 |
| 2c |
| 2a |
| 2 |
故选 A.
点评:本题考查椭圆与抛物线的综合问题.在求椭圆的离心率时,一般是求出a和c,也可以先求出b和c或a,b;再利用a,b,c之间的关系来求离心率e.

练习册系列答案
相关题目
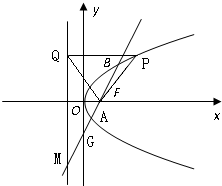 如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形.
如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形. 过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1.
过抛物线焦点垂直于对称轴的弦叫做抛物线的通径.如图,已知抛物线y2=2px(p>0),过其焦点F的直线交抛物线于A(x1,y1)、B(x2,y2)两点,过A、B作准线的垂线,垂足分别为A1、B1. (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,…. 如图,已知抛物线y2=2px(p>0),过它的焦点F的直线l与其相交于A,B两点,O为坐标原点.
如图,已知抛物线y2=2px(p>0),过它的焦点F的直线l与其相交于A,B两点,O为坐标原点.