题目内容
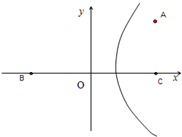
(本题满分14分) 若F1、F2为双曲线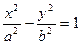 的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足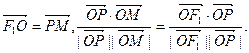 (Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点
(Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点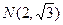 ,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求
,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求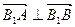 时,直线AB的方程.
时,直线AB的方程.
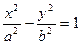 的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足
的左、右焦点,O为坐标原点,P在双曲线左支上,M在右准线上,且满足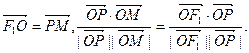 (Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点
(Ⅰ)求此双曲线的离心率;(Ⅱ)若此双曲线过点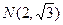 ,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求
,求双曲线方程;(Ⅲ)设(Ⅱ)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求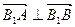 时,直线AB的方程.
时,直线AB的方程.(Ⅰ)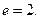 (Ⅱ)
(Ⅱ)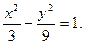 (Ⅲ)
(Ⅲ)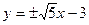
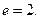 (Ⅱ)
(Ⅱ)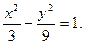 (Ⅲ)
(Ⅲ)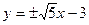
解:(Ⅰ)由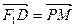 知四边形PF1OM为平行四边形,又由
知四边形PF1OM为平行四边形,又由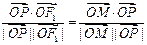
知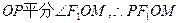 为菱形,设半焦距为c,由
为菱形,设半焦距为c,由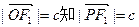 ,
,
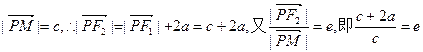
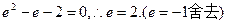
(Ⅱ)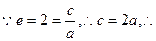 双曲线方程为
双曲线方程为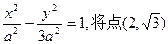 代入,
代入,
有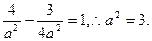 即所求双曲线方程为
即所求双曲线方程为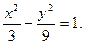
(Ⅲ)依题意得B1(0,3),B2(0,-3).设直线AB的方程为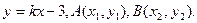
则由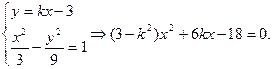 ∵双曲线的渐近线为
∵双曲线的渐近线为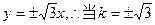 时,AB与双曲线只有一个交点,即
时,AB与双曲线只有一个交点,即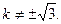
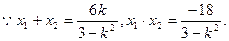
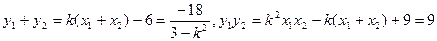
又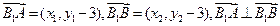
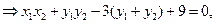
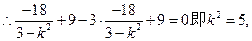
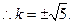 直线AB的方程为
直线AB的方程为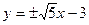
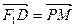 知四边形PF1OM为平行四边形,又由
知四边形PF1OM为平行四边形,又由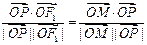
知
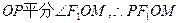 为菱形,设半焦距为c,由
为菱形,设半焦距为c,由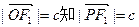 ,
,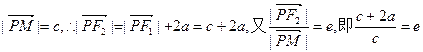
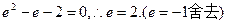
(Ⅱ)
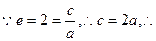 双曲线方程为
双曲线方程为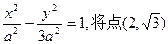 代入,
代入,有
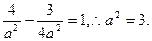 即所求双曲线方程为
即所求双曲线方程为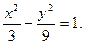
(Ⅲ)依题意得B1(0,3),B2(0,-3).设直线AB的方程为
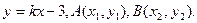
则由
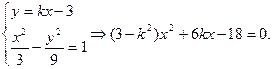 ∵双曲线的渐近线为
∵双曲线的渐近线为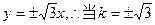 时,AB与双曲线只有一个交点,即
时,AB与双曲线只有一个交点,即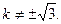
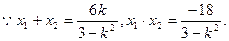
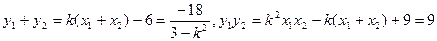
又
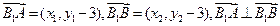
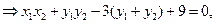
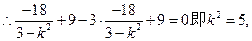
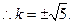 直线AB的方程为
直线AB的方程为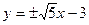

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
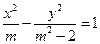 表示焦点在
表示焦点在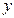 轴上的椭圆,那么实数
轴上的椭圆,那么实数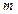 的取值范围是( )
的取值范围是( )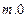
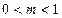
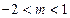
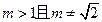
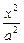 -
-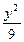 =1上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线的左、右焦点
=1上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线的左、右焦点 若|PF1|=3,则|PF2|等于
若|PF1|=3,则|PF2|等于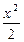 -y2=1有公共渐近线的双曲线方程是
-y2=1有公共渐近线的双曲线方程是 -
- ="1"
="1"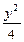 -
-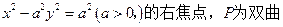 线右支上的一点,
线右支上的一点,
 ( )
( )
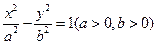 的一个焦点为F,左右顶点分别为A,B .P是双曲线上任意一点,则分别以线段
的一个焦点为F,左右顶点分别为A,B .P是双曲线上任意一点,则分别以线段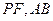 为直径的两圆的位置关系为
为直径的两圆的位置关系为