题目内容
(本题12分)已知函数
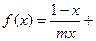 1n
1n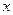 ,且
,且 >0
>0
(Ⅰ)若函数
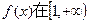 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(Ⅱ)求函数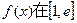 的最大值和最小值。
的最大值和最小值。

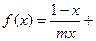 1n
1n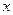 ,且
,且 >0
>0
(Ⅰ)若函数

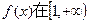 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;(Ⅱ)求函数
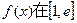 的最大值和最小值。
的最大值和最小值。解(Ⅰ)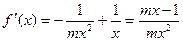
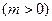 。 ……………1分
。 ……………1分
因为函数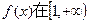 上为增函数,
上为增函数,
所以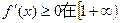 上恒成立,
上恒成立,
所以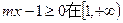 上恒成立,
上恒成立,
所以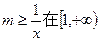 上恒成立。
上恒成立。
所以 的取值范围是
的取值范围是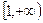 。 ………………3分
。 ………………3分
(Ⅱ)令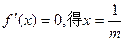
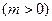 。 ………………4分
。 ………………4分
①若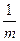
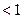 ,即
,即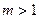 ,则
,则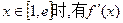
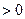 ,
,
所以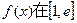 上递增,
上递增,
所以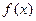 的最大值是
的最大值是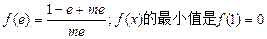 。
。
………………6分
②若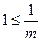
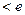 ,即
,即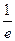
 ,
,
则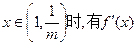
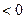 ,所以
,所以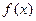 在
在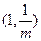 上递减;
上递减;
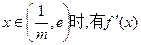
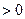 ,所以
,所以 上递增。
上递增。
所以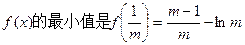 。
。
又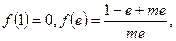
所以当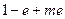
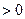 ,即
,即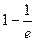
 时,有
时,有
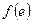
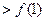 ,
,
所以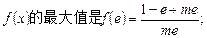
当

所以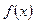 的最大值是
的最大值是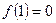 。 ………………9分
。 ………………9分
③若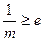 ,即
,即
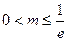 ,则
,则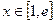 时,有
时,有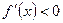 ,
,
所以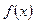 在
在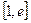 上递增,
上递增,
所以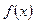 的最大值是
的最大值是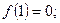
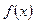 的最小值是
的最小值是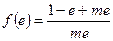 。
。
………………11分
所以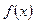 的最大值是
的最大值是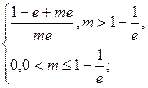
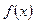 的最小值是
的最小值是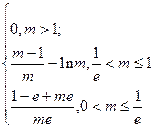
………………12分
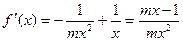
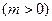 。 ……………1分
。 ……………1分因为函数
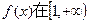 上为增函数,
上为增函数,所以
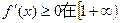 上恒成立,
上恒成立,所以
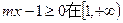 上恒成立,
上恒成立,所以
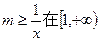 上恒成立。
上恒成立。所以
 的取值范围是
的取值范围是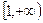 。 ………………3分
。 ………………3分(Ⅱ)令
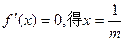
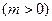 。 ………………4分
。 ………………4分①若
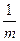
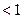 ,即
,即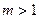 ,则
,则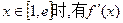
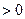 ,
,所以
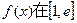 上递增,
上递增,所以
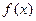 的最大值是
的最大值是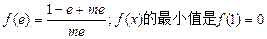 。
。………………6分
②若
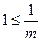
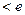 ,即
,即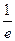
 ,
,则
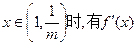
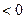 ,所以
,所以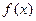 在
在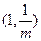 上递减;
上递减;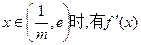
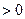 ,所以
,所以 上递增。
上递增。所以
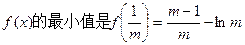 。
。又
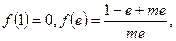
所以当
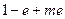
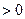 ,即
,即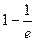
 时,有
时,有
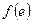
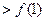 ,
,所以
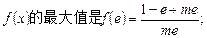
当


所以
 的最大值是
的最大值是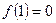 。 ………………9分
。 ………………9分③若
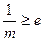 ,即
,即
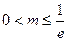 ,则
,则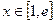 时,有
时,有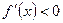 ,
,所以
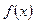 在
在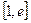 上递增,
上递增,所以
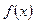 的最大值是
的最大值是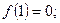
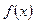 的最小值是
的最小值是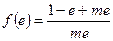 。
。………………11分
所以
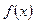 的最大值是
的最大值是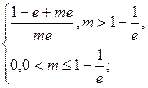
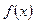 的最小值是
的最小值是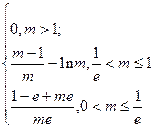
………………12分
略

练习册系列答案
相关题目
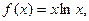
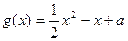 .
.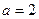 时,求
时,求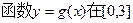 上的值域;
上的值域;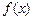 在
在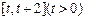 上的最小值;
上的最小值;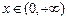 ,都有
,都有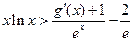 成立
成立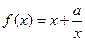 的定义域为
的定义域为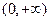 ,且
,且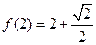 。设点P是函数
。设点P是函数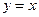 和y轴的垂线,垂足分别为M、N.
和y轴的垂线,垂足分别为M、N.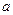 的值;
的值;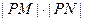 是否为定值?若是,则求出该定值,若不是则说明理由.
是否为定值?若是,则求出该定值,若不是则说明理由.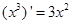 ,
,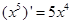 ,
,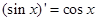 ,由归纳推理可得:若
,由归纳推理可得:若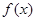 是定义在
是定义在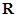 上的奇函数,记
上的奇函数,记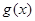 为
为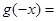
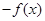
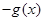
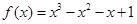 在
在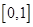 上零点的个数为( )
上零点的个数为( )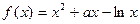 ,
, 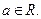
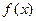 在
在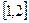 上是减函数,求实数
上是减函数,求实数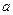 的取值范围
的取值范围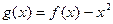 ,是否存在实数
,是否存在实数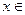
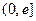 (
(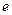 是自然常数)时,函数
是自然常数)时,函数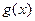 的最小值是3,若存在,求出
的最小值是3,若存在,求出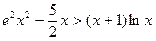
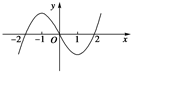
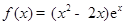 的图象大致是( )
的图象大致是( )