题目内容
设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x·f′(x)的图象的一部分,则f(x)的极大值与极小值分别是
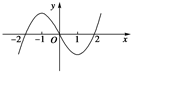
| A.f(1)与f(-1) | B.f(-1)与f(1) | C.f(-2)与f(2) | D.f(2)与f(-2) |

C
分析:当x<0时,f′(x)的符号与x?f′(x)的符号相反;当x>0时,f′(x)的符号与x?f′(x)的符号相反同
由y=x?f′(x)的图象得f′(x)的符号;判断出函数的单调性得函数的极值.
解答:解:由y=x?f′(x)的图象知,
x∈(-∞,-2)时,f′(x)>0;x∈(-2,2)时,f′(x)≤0;x∈(2,+∞)时,,f′(x)>0
∴当x=-2时,f(x)有极大值f(-2);当x=2时,f(x)有极小值f(2)
故选项为C
由y=x?f′(x)的图象得f′(x)的符号;判断出函数的单调性得函数的极值.
解答:解:由y=x?f′(x)的图象知,
x∈(-∞,-2)时,f′(x)>0;x∈(-2,2)时,f′(x)≤0;x∈(2,+∞)时,,f′(x)>0
∴当x=-2时,f(x)有极大值f(-2);当x=2时,f(x)有极小值f(2)
故选项为C

练习册系列答案
相关题目
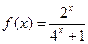
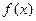 的奇偶性
的奇偶性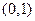 上是减函数
上是减函数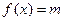 在
在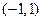 上有解,求
上有解,求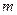 的取值范围?
的取值范围?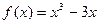 ,若曲线
,若曲线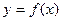 在点A(0,16)处的切线方程为
在点A(0,16)处的切线方程为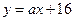 ,则实数
,则实数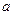 的值是( )
的值是( )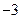
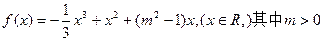
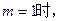 曲线
曲线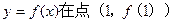 处的切线斜率
处的切线斜率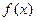 有三个互不相同的零点0,
有三个互不相同的零点0,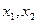 ,且
,且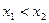 .若对任意的
.若对任意的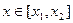 ,
,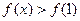 恒成立,求m的取值范围.
恒成立,求m的取值范围.
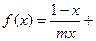 1n
1n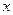 ,且
,且 >0
>0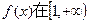 上是增函数,求
上是增函数,求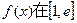 的最大值和最小值。
的最大值和最小值。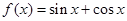 ,
,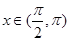 ,
,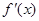 是
是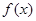 的导函数,若
的导函数,若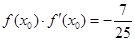 ,则曲线
,则曲线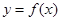 在点
在点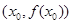 处的切线斜率是( )
处的切线斜率是( )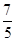
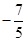
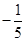
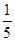
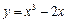 在点(1,-1)处的切线方程是 .
在点(1,-1)处的切线方程是 .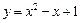 在点(1,0)处的切线方程为 ;
在点(1,0)处的切线方程为 ;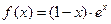 的单调递增区间是
的单调递增区间是  .
.