题目内容
.已知函数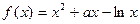 ,
, 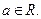
(1)若函数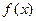 在
在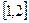 上是减函数,求实数
上是减函数,求实数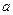 的取值范围
的取值范围
(2)令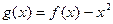 ,是否存在实数
,是否存在实数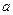 ,当
,当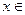
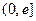 (
(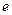 是自然常数)时,函数
是自然常数)时,函数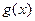 的最小值是3,若存在,求出
的最小值是3,若存在,求出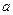 的值;若不存在,说明理由
的值;若不存在,说明理由
(3)当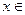
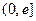 时,证明:
时,证明: 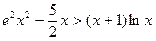
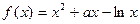 ,
, 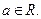
(1)若函数
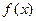 在
在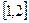 上是减函数,求实数
上是减函数,求实数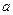 的取值范围
的取值范围(2)令
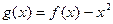 ,是否存在实数
,是否存在实数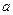 ,当
,当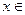
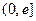 (
(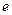 是自然常数)时,函数
是自然常数)时,函数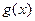 的最小值是3,若存在,求出
的最小值是3,若存在,求出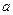 的值;若不存在,说明理由
的值;若不存在,说明理由(3)当
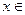
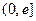 时,证明:
时,证明: 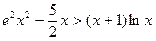
解:(1) 在
在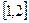 上恒成立
上恒成立
令 ,有
,有 得
得
得
(2)假设存在实数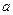 ,使
,使 (
( )有最小值3,
)有最小值3,


①当 时,
时,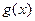 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),
②当 时,
时,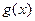 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增

 ,
, ,满足条件
,满足条件
③当 时,
时,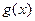 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),
综上,存在实数 ,使得当
,使得当 时
时 有最小值3
有最小值3
(3)令 ,由(2)知
,由(2)知
 .令
.令 ,
,
当 时,
时, ,
, 在
在 上单调递增
上单调递增
∴
 即
即

 在
在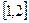 上恒成立
上恒成立令
 ,有
,有 得
得
得

(2)假设存在实数
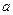 ,使
,使 (
( )有最小值3,
)有最小值3,

①当
 时,
时,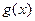 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),②当
 时,
时,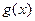 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增
 ,
, ,满足条件
,满足条件③当
 时,
时,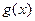 在
在 上单调递减,
上单调递减, ,
, (舍去),
(舍去),综上,存在实数
 ,使得当
,使得当 时
时 有最小值3
有最小值3(3)令
 ,由(2)知
,由(2)知 .令
.令 ,
,
当
 时,
时, ,
, 在
在 上单调递增
上单调递增 ∴

 即
即

略

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
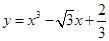 上的任意一点,p点处切线倾斜角为a,则角a的取值范围是( )
上的任意一点,p点处切线倾斜角为a,则角a的取值范围是( )




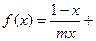 1n
1n ,且
,且 >0
>0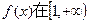 上是增函数,求
上是增函数,求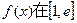 的最大值和最小值。
的最大值和最小值。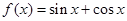 ,
,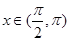 ,
,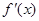 是
是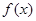 的导函数,若
的导函数,若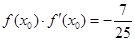 ,则曲线
,则曲线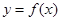 在点
在点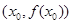 处的切线斜率是( )
处的切线斜率是( )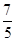
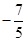
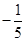
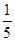
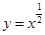 ,②
,②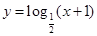 ,③
,③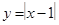 ,④
,④ ,其中在
,其中在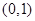 上单调递减的函数序号是( )
上单调递减的函数序号是( )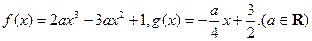
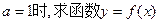 的单调区间;
的单调区间;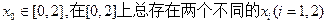 ,使得
,使得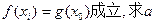 的取值范围。
的取值范围。 在
在 上的最大值和最小值。
上的最大值和最小值。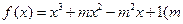 为常数,且
为常数,且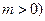 有极大值
有极大值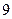 ,求
,求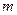 的值及
的值及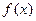 的极小值.
的极小值.