题目内容
观察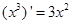 ,
,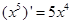 ,
,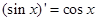 ,由归纳推理可得:若
,由归纳推理可得:若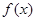 是定义在
是定义在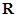 上的奇函数,记
上的奇函数,记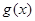 为
为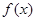 的导函数,则
的导函数,则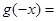
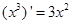 ,
,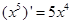 ,
,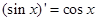 ,由归纳推理可得:若
,由归纳推理可得:若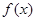 是定义在
是定义在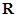 上的奇函数,记
上的奇函数,记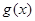 为
为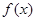 的导函数,则
的导函数,则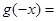
A.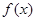 | B.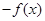 | C.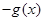 | D.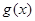 |
D
分析:函数y=x3、y=x5与y=sinx都是定义在R上的奇函数,而它们的导数都是偶函数.由此归纳,得一个奇函数的导数是偶函数,不难得到正确答案.
解答:解:根据(x3)′=3x2、(x5)′=5x4、(sinx)′=cosx,发现原函数都是一个奇函数,它们的导数都是偶函数
由此可得规律:一个奇函数的导数是偶函数.
而定义在R上的函数f(x)满足f(-x)=-f(x),说明函数f(x)是一个奇函数
因此,它的导数应该是一个偶函数,即g(-x)=g(x)
故选D
解答:解:根据(x3)′=3x2、(x5)′=5x4、(sinx)′=cosx,发现原函数都是一个奇函数,它们的导数都是偶函数
由此可得规律:一个奇函数的导数是偶函数.
而定义在R上的函数f(x)满足f(-x)=-f(x),说明函数f(x)是一个奇函数
因此,它的导数应该是一个偶函数,即g(-x)=g(x)
故选D

练习册系列答案
相关题目
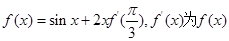 的导函数,令
的导函数,令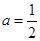 ,
,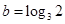 ,则下列关系正确的是( )
,则下列关系正确的是( )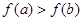
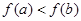
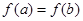
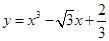 上的任意一点,p点处切线倾斜角为a,则角a的取值范围是( )
上的任意一点,p点处切线倾斜角为a,则角a的取值范围是( )



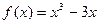 ,若曲线
,若曲线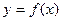 在点A(0,16)处的切线方程为
在点A(0,16)处的切线方程为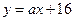 ,则实数
,则实数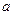 的值是( )
的值是( )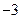
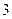
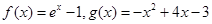 ,若有
,若有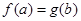 ,则b的取值范围为( )
,则b的取值范围为( )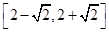
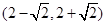
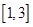
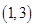

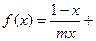 1n
1n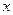 ,且
,且 >0
>0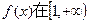 上是增函数,求
上是增函数,求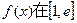 的最大值和最小值。
的最大值和最小值。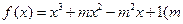 为常数,且
为常数,且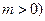 有极大值
有极大值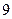 ,求
,求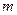 的值及
的值及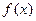 的极小值.
的极小值.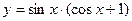 的导数是 。
的导数是 。