题目内容
已知函数f(x)=lg(1+x)-lg(1-x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求方程f(x)=1的解集.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求方程f(x)=1的解集.
考点:对数函数的图像与性质,对数的运算性质
专题:函数的性质及应用
分析:(1)x需满足:
,解得-1<x<1,可得函数的定义域;
(2)计算f(-x),观察是否等于±f(x),再由奇偶性定义即可得到;
(3)方程f(x)=1可化为lg(1+x)-lg(1-x)=1,变形为lg
=1,进一步得出
=10,解方程即可.
|
(2)计算f(-x),观察是否等于±f(x),再由奇偶性定义即可得到;
(3)方程f(x)=1可化为lg(1+x)-lg(1-x)=1,变形为lg
| 1+x |
| 1-x |
| 1+x |
| 1-x |
解答:
解:(1)要使函数有意义,x需满足:
,解得-1<x<1,
所以函数的定义域为(-1,1)
(2)函数f(x)为奇函数.
理由如下:函数f(x)=lg(1+x)-lg(1-x),
∵定义域为(-1,1),∴关于原点对称,
∵f(-x)=lg(1-x)-lg(1+x)=-f(x),
则f(x)为奇函数.
(3)方程f(x)=1可化为lg(1+x)-lg(1-x)=1,
∴lg
=1,∴
=10,解得x=
,
∴方程的解集为{x|x=
}
|
所以函数的定义域为(-1,1)
(2)函数f(x)为奇函数.
理由如下:函数f(x)=lg(1+x)-lg(1-x),
∵定义域为(-1,1),∴关于原点对称,
∵f(-x)=lg(1-x)-lg(1+x)=-f(x),
则f(x)为奇函数.
(3)方程f(x)=1可化为lg(1+x)-lg(1-x)=1,
∴lg
| 1+x |
| 1-x |
| 1+x |
| 1-x |
| 9 |
| 11 |
∴方程的解集为{x|x=
| 9 |
| 11 |
点评:本题考查函数的奇偶性的判断,注意首先考虑函数的定义域是否关于原点对称,考查运算能力,属于基础题和易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
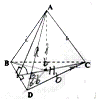 如图,已知空间四边形ABCD,及两条对角线AC、BD,AB=AC=AD=a,BD=DC=CD=b,AB⊥面BCD,垂足为H,求平面ABD与平面BCD所成角的大小.
如图,已知空间四边形ABCD,及两条对角线AC、BD,AB=AC=AD=a,BD=DC=CD=b,AB⊥面BCD,垂足为H,求平面ABD与平面BCD所成角的大小.