题目内容
已知三棱锥A-BCD中，AB=CD，AC=BD，E、F分别是AD、BC的中点，试用向量方法证明EF是AD与BC的公垂线．
考点：向量在几何中的应用
专题：平面向量及应用
分析：由已知中AB=CD，AC=BD，可得
2=
2+
2-2
•
，
2=
2=
2+
2-2
•
，故
2=
2-2
•
+
2+
2-2
•
，整理得2
2-2(
+
)•
=0，即
•(
+
-
)=2
•
=0．进而可得
⊥
，同理可证：
⊥
，进而EF是AD与BC的公垂线．
| AC |
| AB |
| AD |
| AB |
| AD |
| AB |
| CD |
| AC |
| AD |
| AC |
| AD |
| AB |
| AD |
| AC |
| AD |
| AB |
| AD |
| AB |
| AD |
| AD |
| AC |
| AB |
| AD |
| AD |
| AC |
| AB |
| AD |
| AD |
| EF |
| EF |
| AD |
| EF |
| BC |
解答：
证明：如图所示：
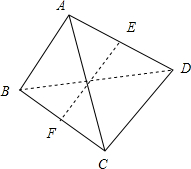
∵F是BC的中点，
∴
=
+
=-
+
+
=
（
+
-
），
又∵AC=BD，
∴|
|=|
|=|
-
|，
∴
2=
2+
2-2
•
，
同理由AB=CD得：
2=
2=
2+
2-2
•
，
故
2=
2-2
•
+
2+
2-2
•
，
∴2
2-2(
+
)•
=0，
∴
•(
+
-
)=2
•
=0．
即
⊥
，
同理可证：
⊥
，
故EF是AD与BC的公垂线．
∵F是BC的中点，
∴
| EF |
| EA |
| AF |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AB |
| AC |
| AD |
又∵AC=BD，
∴|
| AC |
| BD |
| AD |
| AB |
∴
| AC |
| AB |
| AD |
| AB |
| AD |
同理由AB=CD得：
| AB |
| CD |
| AC |
| AD |
| AC |
| AD |
故
| AB |
| AD |
| AC |
| AD |
| AB |
| AD |
| AB |
| AD |
∴2
| AD |
| AC |
| AB |
| AD |
∴
| AD |
| AC |
| AB |
| AD |
| AD |
| EF |
即
| EF |
| AD |
同理可证：
| EF |
| BC |
故EF是AD与BC的公垂线．
点评：本题考查的知识点是向量垂直的充要条件，向量加法的三角形法则，难度中档．
练习册系列答案
相关题目
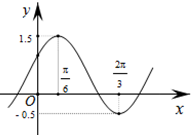已知函数y=Asin（ωx+φ）+b的一部分图象如图所示，若A＞0，ω＞0，|φ|＜