题目内容
14.是否存在实数a,使得f(x)=loga(ax-$\sqrt{x}$) 在[2,4]上是增函数?若存在,求a的取值范围.分析 分类讨论,考查内外函数的单调性,利用f(x)=loga(ax-$\sqrt{x}$)(a>0,且a≠1)在区间[2,4]上是增函数,即可求实数a的取值范围.
解答 解:设t=ax-$\sqrt{x}$=a($\sqrt{x}$-$\frac{1}{2a}$)2-$\frac{1}{4a}$,
当a>1时,由于函数t=ax-$\sqrt{x}$在[2,4]是增函数,且函数t大于0恒成立,
故函数f (x)=loga(ax-$\sqrt{x}$)在[2,4]是增函数,满足条件.
当 1>a>0时,由题意可得函数t=ax-$\sqrt{x}$在[2,4]应是减函数,且函数t大于0,
故$\frac{1}{2a}$≥$\sqrt{4}$,且4a-2>0,此时无解
综上,实数a的取值范围是(1,+∞)
点评 本题考查对数函数的单调性,考查复合函数的单调区间,难度中档.

练习册系列答案
相关题目
2.设x∈R,则“l<x<2”是“l<x<3”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.已知全集为R,集合M={x||x-3|<2},集合N={x|ln(x-2)>0},则M∩(∁RN)=( )
| A. | (3,5) | B. | [3,5) | C. | (1,3) | D. | (1,3] |
3.函数f(x)=ex+x-2的零点所在的区间是(e≈2.71828)( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
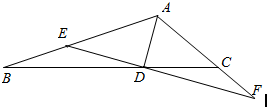 已知△ABC中,AB=2,AC=1,∠BAC=120°,AD为角平分线.
已知△ABC中,AB=2,AC=1,∠BAC=120°,AD为角平分线.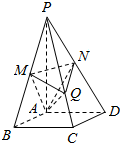 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分别为PB,PD的中点.