题目内容

椭圆C1：
x2
a2
+
y2
b2
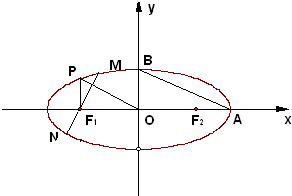
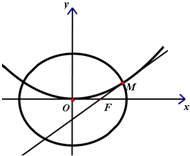
=1(a＞b＞0)与抛物线C2：x2=2py（p＞0）的一个交点为M．抛物线C2在点M处的切线过椭圆C1的右焦点F．
（1）若M(2，
2
5
5
)，求C1和C2的标准方程；
（II）若b=1，求p关于a的函数表达式p=f（a）．
（1）把M(2，
2
5
5
)代入C2：x2=2py（p＞0）得p=
5
，故C2：x2=2
5
y…（2分）
由y=
5
10
x2得y′=
5
5
x，从而C2在点M处的切线方程为y-
2
5
5
=
2
5
5
(x-2)…（4分）
令y=0有x=1，F（1，0），…（5分）
又M在(2，
2
5
5
)椭圆C1上
所以
4
a2
+
4
5b2
=1
a2-b2=1
，解得a2=5，b2=4，故C1：
x2
5
+
y2
4
=1…（7分）
（2）设M(x0，
1
2p
x02)，由y=
1
2p
x2得y′=
1
p
x，
从而C2在点M处的切线方程为y-
x02
2p
=
x0
p
(x-x0)…（9分）
设F（c，0），代入上式得x0=2c，
因为
x02
a2
+
y02
b2
=1，所以y02=b2(1-
x02
a2
)=b2(1-
4c2
a2
)=
b2
a2
(4b2-3a2)…（11分）
又x02=2py0，所以p=
x02
2y0
=
2c2
b
a
4b2-3a2
=
2a(a2-b2)
b
4b2-3a2
=
2a(a2-1)
4-3a2
，…（13分）
结合a＞b知1＜a＜
2
3
3
，所以p=f（a）=
2a(a2-1)
4-3a2
（1＜a＜
2
3
3
）．…（14分）
练习册系列答案
相关题目
已知平面内一点P与两个定点F1(-
3
，0)和F2(
3
，0)的距离的差的绝对值为2．
（Ⅰ）求点P的轨迹方程C；
（Ⅱ）设过（0，-2）的直线l与曲线C交于A，B两点，且OA⊥OB（O为坐标原点），求直线l的方程．
如图，F1，F2是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的焦点，P为椭圆上的点，PF1⊥OX轴，且OP和椭圆的一条长轴顶点A和短轴顶点B的连线AB平行．
（1）求椭圆的离心率e
（2）若Q是椭圆上任意一点，证明∠F1QF2≤
π
2

（3）过F1与OP垂直的直线交椭圆于M，N，若△MF2N的面积为20
3
，求椭圆方程．
设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右顶点分别为A（-
2
，0）、B（
2
，0），离心率e=
2
2
．过该椭圆上任一点P作PQ⊥x轴，垂足为Q，点C在QP的延长线上，且|PC|=（
2
-1）|PQ|．
（1）求椭圆的方程；
（2）求动点C的轨迹E的方程；
（3）设直线MN过椭圆的右焦点与椭圆相交于M、N两点，且|MN|=
8
2
7
，求直线MN的方程．
已知斜率为1的直线l过椭圆
x2
4
+y2=1的右焦点F2．
（1）求直线l的方程；
（2）若l与椭圆交于点A、B两点，F1为椭圆左焦点，求S△F1AB．
已知椭圆C过点P（1，
3
2
），两个焦点分别为F1（-1，0），F2（1，0）．
（1）求椭圆C的方程；
（2）过点F1的直线交椭圆于A、B两点，求线段AB的中点的轨迹方程．
如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)过点(1，
2
2
)，离心率为
2
2
，左、右焦点分别为F1、F2．点P为直线l：x+y=2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点．设直线PF1、PF2的斜率分别为k1、k2．
（Ⅰ）证明：
1
k1
-
3
k2
=2；
（Ⅱ）问直线l上是否存在点P，使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0？若存在，求出所有满足条件的点P的坐标；若不存在，说明理由．
如图，已知圆C1的方程为(x-2)2+(y-1)2=
20
3
，椭圆C2的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），C2的离心率为
2
2
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，求直线AB的方程和椭圆C2的方程．
已知椭圆C1：
x2
4
+
y2
3
=1和抛物线C2：y2=2px（p＞0），过点M（1，0）且倾斜角为
π
3
的直线与抛物线交于A、B，与椭圆交于C、D，当|AB|：|CD|=5：3时，求p的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网