题目内容
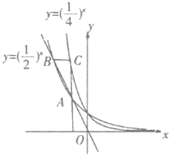 如图,过原点O的直线与函数y=(
如图,过原点O的直线与函数y=(| 1 |
| 2 |
| 1 |
| 4 |
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:先设A(n,2-n),B(m,2-m),则由过B作y轴的垂线交函数y=(
)x的图象于点C写出点C的坐标,再依据AC平行于y轴得出m,n之间的关系:n=
,最后根据A,B,O三点共线.利用斜率相等即可求得点A的坐标.
| 1 |
| 4 |
| m |
| 2 |
解答:
解:设A(n,2-n),B(m,2-m),
由4-x=2-m=2-2x,即m=2x,
解得x=
,即C(
,2-m).
∵AC平行于y轴,
∴n=
,m=2n,
∴A(
,2-n),B(m,2-m),
又A,B,O三点共线.
∴kOA=kOB,
∴
=
,
∴n=m+1.
∴
=m+1,
解得m=-2,
∴n=-1,
∴故点A的坐标是(-1,2)
故答案为:(-1,2)
由4-x=2-m=2-2x,即m=2x,
解得x=
| m |
| 2 |
| m |
| 2 |
∵AC平行于y轴,
∴n=
| m |
| 2 |
∴A(
| m |
| 2 |
又A,B,O三点共线.
∴kOA=kOB,
∴
| 2-n | ||
|
| 2-m |
| m |
∴n=m+1.
∴
| m |
| 2 |
解得m=-2,
∴n=-1,
∴故点A的坐标是(-1,2)
故答案为:(-1,2)
点评:本题主要考查了指数函数的图象与性质、直线的斜率公式、三点共线的判定方法等,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a,b,c成等比数列,则函数y=ax2+bx+
的图象与x轴交点个数是( )
| c |
| 4 |
| A、0 | B、1 | C、2 | D、0或2 |
 如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k
如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k 如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且
如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且