题目内容
设函数f(x)=A(sinωx+cosωx)(A>0,ω>0),正确的有
①f(x)的最大值为A;
②f(x)的最小正周期为
;
③函数f(x)在区间[0,
]上是增函数;
④若f(x)的图象的一条对称轴是直线x=
,且f(x)在区间[
,
]上是单调的,则ω=2;
⑤若f(
)=f(
),则f(x)的图象关于直线x=
对称”.
①f(x)的最大值为A;
②f(x)的最小正周期为
| 2π |
| ω |
③函数f(x)在区间[0,
| π |
| 4 |
④若f(x)的图象的一条对称轴是直线x=
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
⑤若f(
| π |
| 8 |
| 3π |
| 8 |
| π |
| 4 |
考点:正弦函数的单调性,三角函数的周期性及其求法,正弦函数的对称性
专题:三角函数的图像与性质
分析:由条件利用正弦函数的最值、周期性、图象的对称性、单调性,对各个结论的正确性作出判断,从而得出结论.
解答:
解:由于函数f(x)=A(sinωx+cosωx)=A
sin(ωx+
) (A>0,ω>0),
可得它的最大值为
A,故①不对.
可得它的最小正周期为
,故②正确.
根据ω不确定,故不能确定函数f(x)在区间[0,
]上的单调性,故③不正确.
若f(x)的图象的一条对称轴是直线x=
,则ω•
+
=kπ+
,即ω=8k+2,k∈z;
再由f(x)在区间[
,
]上是单调的,可得
-
≤
•
,即0<ω≤8,则ω=2,故④正确.
若f(
)=f(
),则f(x)的图象关于直线x=
=
对称,故⑤正确,
故答案为:②④⑤.
| 2 |
| π |
| 4 |
可得它的最大值为
| 2 |
可得它的最小正周期为
| 2π |
| ω |
根据ω不确定,故不能确定函数f(x)在区间[0,
| π |
| 4 |
若f(x)的图象的一条对称轴是直线x=
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
再由f(x)在区间[
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| 1 |
| 2 |
| 2π |
| ω |
若f(
| π |
| 8 |
| 3π |
| 8 |
| ||||
| 2 |
| π |
| 4 |
故答案为:②④⑤.
点评:本题主要考查正弦函数的最值、周期性、图象的对称性、单调性,属于基础题.

练习册系列答案
相关题目
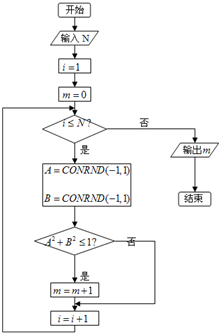 如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )
如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )| A、3.141 |
| B、3.142 |
| C、3.151 |
| D、3.152 |
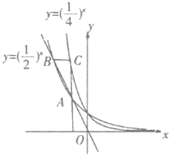 如图,过原点O的直线与函数y=(
如图,过原点O的直线与函数y=(