题目内容
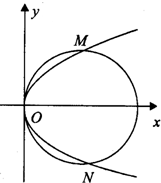 如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且
如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且| OM |
| ON |
(1)求曲线c1的方程;
(2)过定点M(3,2)的直线l与曲线c1交于A,B两点,若点M是线段AB的中点,求线段AB的长.
考点:直线与圆锥曲线的综合问题,平面向量数量积的运算
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由对称性知MN⊥x轴于点(6,0),且|MN|=12,可得M的坐标,代入抛物线方程,即可求曲线c1的方程;
(2)利用点差法求出直线AB的斜率,可得AB的方程,与抛物线方程联立,结合弦长公式,可求线段AB的长度.
(2)利用点差法求出直线AB的斜率,可得AB的方程,与抛物线方程联立,结合弦长公式,可求线段AB的长度.
解答:
 解:(1)由对称性知MN⊥x轴于点(6,0),且|MN|=12
解:(1)由对称性知MN⊥x轴于点(6,0),且|MN|=12
所以M(6,6),…(3分)
所以62=2p×6
所以p=3…(4分)
所以曲线为y2=6x…(5分)
(2)设A(x1,y1),B(x2,y2)
因为(3,2)是AB中点
所以x1+x2=6,y1+y2=4…(6分)
则由点差法得k=
=
…(8分)
所以直线l:3x-2y-5=0
由
得y2-4y-10=0
所以由韦达定理
…(10分)
所以|AB|=
=
…(12分)
 解:(1)由对称性知MN⊥x轴于点(6,0),且|MN|=12
解:(1)由对称性知MN⊥x轴于点(6,0),且|MN|=12所以M(6,6),…(3分)
所以62=2p×6
所以p=3…(4分)
所以曲线为y2=6x…(5分)
(2)设A(x1,y1),B(x2,y2)
因为(3,2)是AB中点
所以x1+x2=6,y1+y2=4…(6分)
则由点差法得k=
| y2-y1 |
| x2-x1 |
| 3 |
| 2 |
所以直线l:3x-2y-5=0
由
|
所以由韦达定理
|
所以|AB|=
(1+
|
2
| ||
| 3 |
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查点差法的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
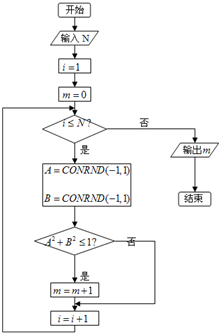 如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )
如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )| A、3.141 |
| B、3.142 |
| C、3.151 |
| D、3.152 |
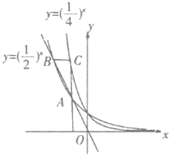 如图,过原点O的直线与函数y=(
如图,过原点O的直线与函数y=(