题目内容
某班有6名班干部,其中男生4人,女生2人,任选3人参加学校的义务劳动.
(1)设所选3人中女生人数为X,求X的分布列;
(2)求X的数学期望.
(1)设所选3人中女生人数为X,求X的分布列;
(2)求X的数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:由已知得X的所有可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答:
(本小题满分14分)
解:(1)由已知得X的所有可能取值为0,1,2,
依题意,得:
P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
∴X的分布列为:
(2)EX=0×
+1×
+2×
=1.
解:(1)由已知得X的所有可能取值为0,1,2,
依题意,得:
P(X=0)=
| ||
|
| 1 |
| 5 |
P(X=1)=
| ||||
|
| 3 |
| 5 |
P(X=2)=
| ||||
|
| 1 |
| 5 |
∴X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
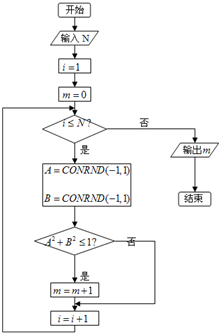 如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )
如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )| A、3.141 |
| B、3.142 |
| C、3.151 |
| D、3.152 |
已知0<a<b,且a+b=1,下列不等式中,一定成立的是( )
①log2a>-1;②log2a+log2b>-2;③log2(b-a)<0;④log2(
+
)>1.
①log2a>-1;②log2a+log2b>-2;③log2(b-a)<0;④log2(
| b |
| a |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、①④ |
已知直线2ax-by+2=0(a>0,b>0)平分圆C:x2+y2+2x-4y+1=0的圆周长,则
+
的最小值为( )
| 1 |
| a |
| 2 |
| b |
A、4
| ||
B、3+2
| ||
| C、4 | ||
| D、6 |
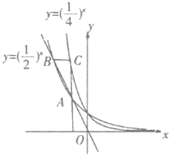 如图,过原点O的直线与函数y=(
如图,过原点O的直线与函数y=(