题目内容
对定义在区间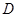 上的函数
上的函数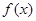 ,若存在闭区间
,若存在闭区间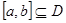 和常数
和常数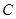 ,使得对任意的
,使得对任意的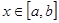 ,都有
,都有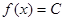 ,且对任意的
,且对任意的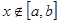 都有
都有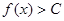 恒成立,则称函数
恒成立,则称函数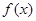 为区间
为区间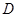 上的“
上的“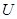 型”函数.
型”函数.
(1)求证:函数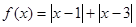 是
是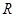 上的“
上的“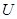 型”函数;
型”函数;
(2)设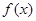 是(1)中的“
是(1)中的“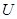 型”函数,若不等式
型”函数,若不等式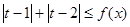 对一切的
对一切的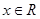 恒成立,求实数
恒成立,求实数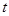 的取值范围;
的取值范围;
(3)若函数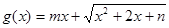 是区间
是区间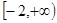 上的“
上的“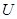 型”函数,求实数
型”函数,求实数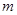 和
和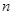 的值.
的值.
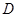 上的函数
上的函数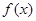 ,若存在闭区间
,若存在闭区间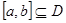 和常数
和常数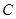 ,使得对任意的
,使得对任意的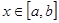 ,都有
,都有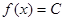 ,且对任意的
,且对任意的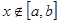 都有
都有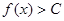 恒成立,则称函数
恒成立,则称函数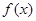 为区间
为区间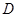 上的“
上的“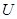 型”函数.
型”函数.(1)求证:函数
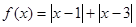 是
是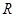 上的“
上的“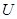 型”函数;
型”函数;(2)设
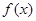 是(1)中的“
是(1)中的“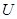 型”函数,若不等式
型”函数,若不等式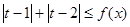 对一切的
对一切的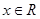 恒成立,求实数
恒成立,求实数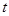 的取值范围;
的取值范围;(3)若函数
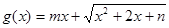 是区间
是区间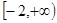 上的“
上的“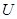 型”函数,求实数
型”函数,求实数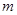 和
和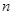 的值.
的值.(1)详见解析;(2)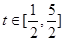 ;(3)
;(3) .
.
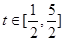 ;(3)
;(3) .
.试题分析:(1)根据题意可将函数中的绝对值去掉可得一个分段函数
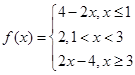 ,可作出函数的图象,不难发现当
,可作出函数的图象,不难发现当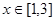 时,
时, ;当
;当 时,
时,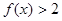 ,由此可易得证; (2)由(1)中的函数不难求出函数的最小值,这们即可将问题转化为求
,由此可易得证; (2)由(1)中的函数不难求出函数的最小值,这们即可将问题转化为求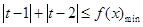 恒成立,这是一个关于
恒成立,这是一个关于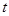 的含有绝对值的不等式,去掉绝对值可得
的含有绝对值的不等式,去掉绝对值可得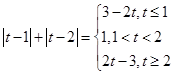 ,然后采用先分开后合并的方法求出此不等式的解集; (3)根据题中“
,然后采用先分开后合并的方法求出此不等式的解集; (3)根据题中“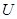 型”函数的定义,则可假设存在闭区间
型”函数的定义,则可假设存在闭区间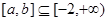 和常数
和常数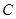 ,使得对任意的
,使得对任意的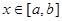 ,都有
,都有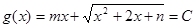 ,这样即可得到一个恒等式,即
,这样即可得到一个恒等式,即 对任意
对任意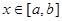 恒成立,则对应系数分别相等,即可求出对应的
恒成立,则对应系数分别相等,即可求出对应的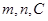 ,注意要回代检验一下,判断其余的是否均大于这个最小值.
,注意要回代检验一下,判断其余的是否均大于这个最小值.试题解析:(1)当
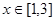 时,
时, ;当
;当 时,
时,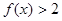 ,
,∴ 存在闭区间
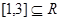 和常数
和常数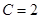 符合条件. 4分
符合条件. 4分(2)
 对一切的
对一切的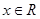 恒成立,
恒成立,∴
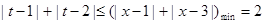 , 6分
, 6分解得
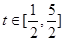 . 10分
. 10分(3)存在闭区间
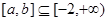 和常数
和常数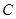 ,使得对任意的
,使得对任意的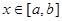 ,
,都有
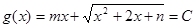 ,即
,即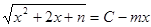 ,
,∴
 对任意
对任意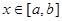 恒成立
恒成立∴
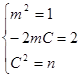
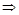
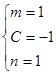 或
或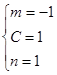 12分
12分① 当
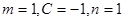 时,
时,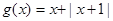
当
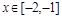 时,
时,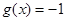
当
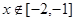 ,即
,即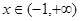 时,
时,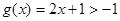
由题意知,
 符合条件; 14分
符合条件; 14分②当
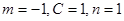 时,
时, 
∴
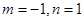 不符合要求; 16分
不符合要求; 16分综上,
 .
.
练习册系列答案
相关题目
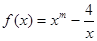 的图象过点(2,0).
的图象过点(2,0).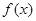 的奇偶性;
的奇偶性;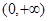 上的单调性,并给予证明;
上的单调性,并给予证明;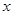 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当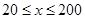 时,车流速度
时,车流速度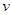 是车流密度x的一次函数.
是车流密度x的一次函数.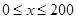 时,求函数
时,求函数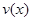 的表达式;
的表达式; 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)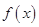 是定义在
是定义在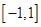 上的奇函数,在
上的奇函数,在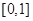 上时
上时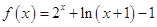
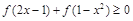 .
.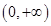 上的函数
上的函数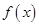 ,如果对任意
,如果对任意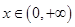 ,恒有
,恒有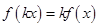 (
(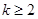 ,
,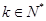 )成立,则称
)成立,则称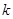 阶缩放函数.
阶缩放函数.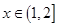 时,
时,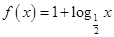 ,求
,求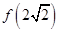 的值;
的值;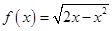 ,求证:函数
,求证:函数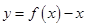 在
在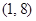 上无零点;
上无零点;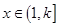 时,
时,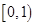 ,求
,求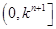 (
(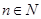 )上的取值范围.
)上的取值范围.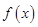 是定义域为
是定义域为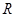 的单调减函数,且是奇函数,当
的单调减函数,且是奇函数,当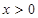 时,
时,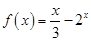
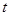 的不等式
的不等式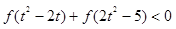
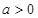 ,
,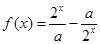 是
是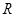 上的奇函数.
上的奇函数.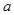 的值;
的值;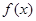 在
在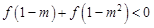 .
.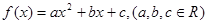 的最小值为
的最小值为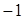 ,且关于
,且关于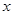 的一元二次不等式
的一元二次不等式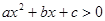 的解集为
的解集为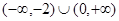 。
。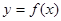 的解析式;
的解析式;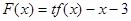 其中
其中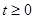 ,求函数
,求函数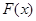 在
在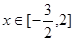 时的最大值
时的最大值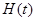 ;
;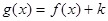 (
(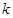 为实数),对任意
为实数),对任意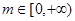 ,总存在
,总存在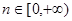 使得
使得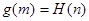 成立,求实数
成立,求实数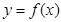 是定义在
是定义在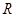 上的偶函数,且在
上的偶函数,且在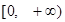 上单调递增,则满足
上单调递增,则满足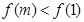 的实数
的实数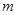 的范围是 .
的范围是 .