题目内容
已函数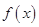 是定义在
是定义在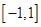 上的奇函数,在
上的奇函数,在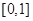 上时
上时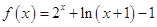
(Ⅰ)求函数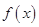 的解析式;
的解析式;
(Ⅱ)解不等式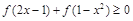 .
.
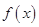 是定义在
是定义在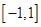 上的奇函数,在
上的奇函数,在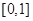 上时
上时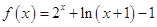
(Ⅰ)求函数
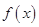 的解析式;
的解析式;(Ⅱ)解不等式
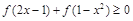 .
.(Ⅰ)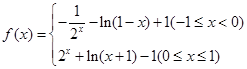 ;(Ⅱ)[0,1]
;(Ⅱ)[0,1]
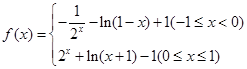 ;(Ⅱ)[0,1]
;(Ⅱ)[0,1]试题分析:(Ⅰ)由奇函数及在[0,1]上的解析式可得函数在[-1,0]上的解析式.从而即可得在[-1,1]上的解析式.本小题主要是考查分段函数的解析式问题.
(Ⅱ)由题意可知函数f(x)在[-1,1]上是递增函数.又因为函数f(x)是奇函数.所以通过
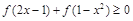 可得.
可得.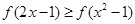 所以可得
所以可得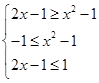 .从而可解得结论.本小题关键是通过函数的单调递增把函数值的大小转化为自变量的大小比较.
.从而可解得结论.本小题关键是通过函数的单调递增把函数值的大小转化为自变量的大小比较.试题解析:(Ⅰ)设
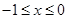 .则
.则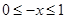 .所以
.所以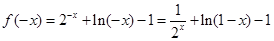 .又f(x)是奇函数.所以f(-x)="-f(x).f(x)=-f(-x)="
.又f(x)是奇函数.所以f(-x)="-f(x).f(x)=-f(-x)=" 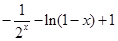 .所以
.所以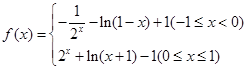 .
.(Ⅱ)易知f(x)是[-1,1]上增函数.由已知得
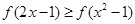 .等价于
.等价于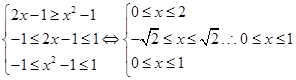 .所以不等式的解集为[0,1].
.所以不等式的解集为[0,1].
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
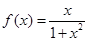 是定义在
是定义在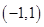 上的函数
上的函数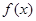 的奇偶性;
的奇偶性;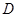 上的函数
上的函数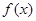 ,若存在闭区间
,若存在闭区间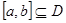 和常数
和常数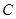 ,使得对任意的
,使得对任意的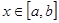 ,都有
,都有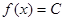 ,且对任意的
,且对任意的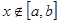 都有
都有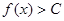 恒成立,则称函数
恒成立,则称函数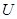 型”函数.
型”函数.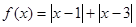 是
是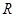 上的“
上的“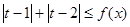 对一切的
对一切的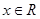 恒成立,求实数
恒成立,求实数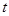 的取值范围;
的取值范围;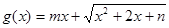 是区间
是区间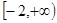 上的“
上的“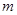 和
和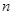 的值.
的值.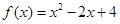 的单调减区间是 .
的单调减区间是 .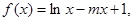 其中
其中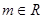 ,
,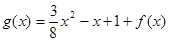 .
.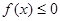 在
在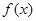 的定义域内恒成立,则实数
的定义域内恒成立,则实数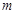 的取值范围 ;
的取值范围 ;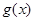 在
在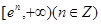 上有零点,则
上有零点,则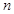 的最大值为 .
的最大值为 .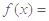
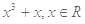 ,当
,当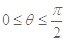 时,
时,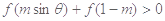 恒成立,则实数
恒成立,则实数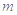 的取值范围是( )
的取值范围是( )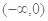
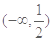
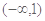
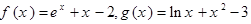 ,若实数
,若实数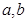 满足
满足 ,则( )
,则( )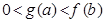
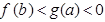
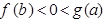
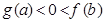
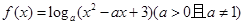 满足:对任意实数
满足:对任意实数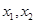 ,当
,当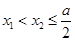 时,总有
时,总有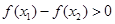 ,则实数
,则实数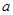 的取值范围是( )
的取值范围是( )
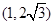
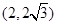
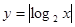 的单调递减区间是 .
的单调递减区间是 .