Question

【题目】如图，在四棱锥E﹣ABCD中，平面EAD⊥平面ABCD，DC∥AB，BC⊥CD，且AB=4，BC=CD=ED=EA=2．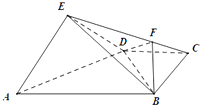
（1）求二面角E﹣AB﹣D的正切值；
（2）在线段CE上是否存在一点F，使得平面EDC⊥平面BDF？若存在，求 的值，若不存在请说明理由．

Answer 1

【答案】
（1）解：取AD的中点H，则EH⊥AD，

又平面EAD⊥平面ABCD，

∴EH⊥平面ABCD，

过H作HN⊥AB于N，由EN⊥AB，

∴∠ENH为二面角E﹣AB﹣D的平面角，

又∵BC⊥AB，AB∥CD，AB=2CD=4，

∴AD=2 ，AH= ，AE=2，∴EH= ，

又HN=1，∴tan ，

∴二面角E﹣AB﹣D的正切值为

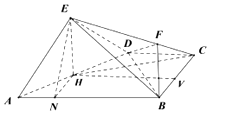
（2）解：存在点F满足条件．

取AB的中点M，由DM= AB，故DB⊥AD，

又平面EAD⊥平面ABCD，

∴BD⊥平面EAD，∴BD⊥ED，

要使平面EDC⊥平面BDF，

在等腰△DEC，DE=DC=2，EC= =2 ，

∴∠DEC=30°，∴EF= ．

∴ = ．

【解析】（1）取AD的中点H，则EH⊥AD，EH⊥平面ABCD，过H作HN⊥AB于N，由EN⊥AB，得∠ENH为二面角E﹣AB﹣D的平面角，由此能求出二面角E﹣AB﹣D的正切值．（2）取AB的中点M，推导出DB⊥AD，BD⊥ED，由此能求出 的值．
【考点精析】通过灵活运用平面与平面垂直的性质，掌握两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直即可以解答此题．