题目内容
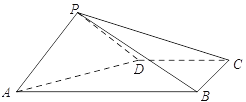
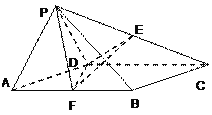
【题目】(2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
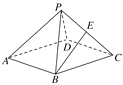
A. BE∥平面PAD,且BE到平面PAD的距离为![]()
B. BE∥平面PAD,且BE到平面PAD的距离为![]()
C. BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D. BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
【答案】D
【解析】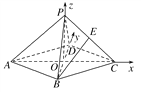
连接AC,BD,交点为O,连接OP,以O为坐标原点,OC,OD,OP所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系,由正四棱锥P-ABCD的棱长均为2,点E为PC的中点,知A(-![]() ,0,0),B(0,-
,0,0),B(0,- ![]() ,0),C(
,0),C(![]() ,0,0),D(0,
,0,0),D(0, ![]() ,0),P(0,0,
,0),P(0,0, ![]() ),E
),E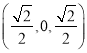 ,则
,则![]() =
= ,
, ![]() =(-
=(-![]() ,0,-
,0,- ![]() ),
), ![]() =(0,
=(0, ![]() ,-
,- ![]() ),设m=(x,y,z)是平面PAD的法向量,则m⊥
),设m=(x,y,z)是平面PAD的法向量,则m⊥![]() ,且m⊥
,且m⊥![]() ,即
,即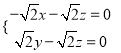 ,令x=1,则z=-1,y=-1,m=(1,-1,-1)是平面PAD的一个法向量,设BE与平面PAD所成的角为θ,则sinθ=
,令x=1,则z=-1,y=-1,m=(1,-1,-1)是平面PAD的一个法向量,设BE与平面PAD所成的角为θ,则sinθ=![]() ,故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°,故选D.
,故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°,故选D.

练习册系列答案
相关题目