题目内容
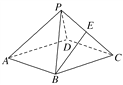
【题目】如图,菱形![]() 与等边
与等边![]() 所在的平面相互垂直,
所在的平面相互垂直, ![]() ,点E,F分别为PC和AB的中点.
,点E,F分别为PC和AB的中点.
(Ⅰ)求证:EF∥平面PAD
(Ⅱ)证明: ![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]() .
.
【解析】试题分析:(I)设![]() 的中点
的中点![]() ,连结
,连结![]() 和
和![]() ,由中位线定理可得
,由中位线定理可得![]() ,从而四边形
,从而四边形![]() 为平行四边形,
为平行四边形, ![]() ,由线面平行的判定定理可得结论;(Ⅱ)由
,由线面平行的判定定理可得结论;(Ⅱ)由![]() 为等边三角形得
为等边三角形得![]() ,由四边形
,由四边形![]() 为菱形,可得
为菱形,可得![]() ,从而
,从而![]() 平面
平面![]() ,进而可得结论;(Ⅲ)根据“等积变换”可得
,进而可得结论;(Ⅲ)根据“等积变换”可得![]() ,由面面垂直的性质可得
,由面面垂直的性质可得![]() 平面
平面![]() ,∴
,∴![]() 为三棱锥
为三棱锥![]() 的高,根据棱锥的体积公式可得结果.
的高,根据棱锥的体积公式可得结果.
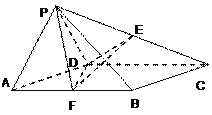
试题解析:(Ⅰ)取PD的中点G,连结GE和GA,
则![]() ,
, ![]() ∴
∴![]()
∴四边形AFEG为平行四边形,∴![]()
∵![]() 平面PAD,EF
平面PAD,EF![]() 平面PAD
平面PAD
∴EF∥平面PAD
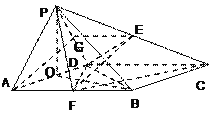
(Ⅱ)取![]() 中点
中点![]() ,连结
,连结![]() ,
,
因为![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
因为四边形![]() 为菱形,所以
为菱形,所以![]() ,
,
又因为![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,
所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(Ⅲ)连结FC,∵PE=EC,∴![]()
∵四边形![]() 为菱形,且
为菱形,且![]() ,
,
∴![]()
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 为三棱锥
为三棱锥![]() 的高.
的高.
∴![]() ,
,
∴![]() .
.
∴![]()
【方法点晴】本题主要考查线面平行的判定定理、面面垂直的性质、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 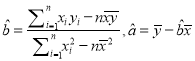 .
.
参考数据: ![]() .
.