题目内容
请你设计一个包装盒,如图所示, 是边长为
是边长为 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
.
(1)若广告商要求包装盒侧面积 最大,试问
最大,试问 应取何值?
应取何值?
(2)若广告商要求包装盒容积 最大,试问
最大,试问 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.


 是边长为
是边长为 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
.(1)若广告商要求包装盒侧面积
 最大,试问
最大,试问 应取何值?
应取何值?(2)若广告商要求包装盒容积
 最大,试问
最大,试问 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.

(1)当 时,
时, 取得最大值;(2)当
取得最大值;(2)当 时取得极大值,也是最大值,此时包装盒的高与底面边长的比值为
时取得极大值,也是最大值,此时包装盒的高与底面边长的比值为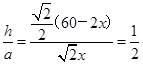 .
.
 时,
时, 取得最大值;(2)当
取得最大值;(2)当 时取得极大值,也是最大值,此时包装盒的高与底面边长的比值为
时取得极大值,也是最大值,此时包装盒的高与底面边长的比值为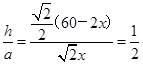 .
.试题分析:(1)先设包装盒的高为
 ,底面边长为
,底面边长为 ,写出
,写出 ,
, 与
与 的关系式,并注明
的关系式,并注明 的取值范围,再利用侧面积公式表示出包装盒侧面积
的取值范围,再利用侧面积公式表示出包装盒侧面积 关于
关于 的函数解析式,最后求出何时它取得最大值即可;
的函数解析式,最后求出何时它取得最大值即可;(2)利用体积公式表示出包装盒容积
 关于
关于 的函数解析式,利用导数知识求出何时它取得的最大值即可.
的函数解析式,利用导数知识求出何时它取得的最大值即可.设包装盒的高为
 ,底面边长为
,底面边长为
由已知得

(1)∵
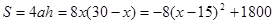 2分
2分∴当
 时,
时, 取得最大值 3分
取得最大值 3分(2)根据题意有
 5分
5分∴
 。
。由
 得,
得, (舍)或
(舍)或 。
。∴当
 时
时 ;当
;当 时
时 7分
7分∴当
 时取得极大值,也是最大值,此时包装盒的高与底面边长的比值为
时取得极大值,也是最大值,此时包装盒的高与底面边长的比值为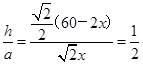
即包装盒的高与底面边长的比值为
 10分.
10分.
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 (a≠0)满足
(a≠0)满足 ,
, 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数 的一个零点.又
的一个零点.又 (
( >0).
>0).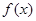 的解析式;
的解析式; 在
在 上有解,求实数
上有解,求实数 ,求
,求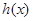 的单调区间.
的单调区间.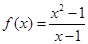 ,
,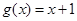 ;②
;②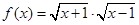 ,
,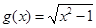 ;③
;③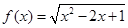 ,
,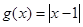 ;④
;④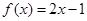 ,
,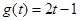 .其中表示同一个函数的有( ).
.其中表示同一个函数的有( ). 、
、 满足
满足 ,则称
,则称 上的一组正交函数,给出三组函数:①
上的一组正交函数,给出三组函数:① ;②
;② ;③
;③ .
. 对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )
对称。据此可推测对任意的非0实数a、b、c、m、n、g关于x的方程m[f(x)]2+n f(x)+g=0的解集不可能是( )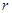 米,高为
米,高为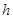 米,体积为
米,体积为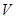 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为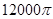 元(
元(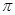 为圆周率).
为圆周率).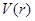 ,并求该函数的定义域;
,并求该函数的定义域; (a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________.
(a+b-|a-b|),如果函数f(x)=-x2+2x+3,g(x)=x+1,那么函数G(x)=F(f(x),g(x))的最大值等于________.