题目内容
已知函数 (a≠0)满足
(a≠0)满足 ,
, 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数 的一个零点.又
的一个零点.又 (
( >0).
>0).
(1)求函数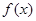 的解析式;
的解析式;
(2)若关于x 的方程 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)令 ,求
,求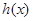 的单调区间.
的单调区间.
 (a≠0)满足
(a≠0)满足 ,
, 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数 的一个零点.又
的一个零点.又 (
( >0).
>0).(1)求函数
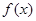 的解析式;
的解析式;(2)若关于x 的方程
 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;(3)令
 ,求
,求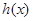 的单调区间.
的单调区间.(1)函数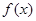 的解析式为
的解析式为 ; (2)实数
; (2)实数 的取值范围为
的取值范围为 ;
;
(3)当 时,
时,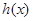 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,
时,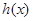 的单调递减区间为
的单调递减区间为 和
和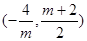 ;
;
单调递增区间为 和
和 .
.
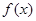 的解析式为
的解析式为 ; (2)实数
; (2)实数 的取值范围为
的取值范围为 ;
;(3)当
 时,
时,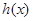 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 时,
时,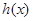 的单调递减区间为
的单调递减区间为 和
和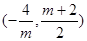 ;
;单调递增区间为
 和
和 .
. 试题分析:(1)由
 得
得 ,又
,又 为偶函数,
为偶函数, 是函数
是函数 的一个零点,得出关于
的一个零点,得出关于 的方程,即可求函数
的方程,即可求函数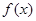 的解析式;
的解析式;(2)
 在
在 上有解,等价于
上有解,等价于 在
在 上有解,可求实数
上有解,可求实数 的取值范围;
的取值范围;(3)先求出
 的解析式,再分
的解析式,再分 、
、 两种情况求出
两种情况求出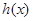 的单调区间.
的单调区间.(1)由
 得
得 1分
1分∵
 即
即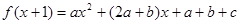
又∵
 为偶函数 ∴
为偶函数 ∴ ① 2分
① 2分∵
 是函数
是函数 的一个零点 ∴
的一个零点 ∴ ∴
∴ ②
②解①②得a=1,b=-2
∴
 4分
4分(2)
 在
在 上有解,即
上有解,即 在
在 上有解.
上有解.∴

∵
 在
在 上单调递增
上单调递增∴实数
 的取值范围为
的取值范围为 8分
8分(3)
 即
即 9分
9分①当
 时,
时, 的对称轴为
的对称轴为
∵m>0 ∴
 总成立
总成立 ∴
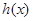 在
在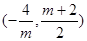 单调递减,在
单调递减,在 上单调递增. 11分
上单调递增. 11分②当
 时,
时, 的对称轴为
的对称轴为
若
 即
即 ,
,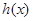 在
在 单调递减 13分
单调递减 13分若
 即
即 ,
,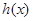 在
在 单调递减,在
单调递减,在 上单调递增. 15分
上单调递增. 15分综上,
当
 时,
时,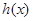 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 时,
时,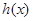 的单调递减区间为
的单调递减区间为 和
和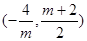 ;单调递增区间为
;单调递增区间为 和
和 . 16分
. 16分
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目


 时,
时,
 的最大值为
的最大值为 ,求
,求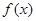 的最小值;
的最小值; ,总有
,总有 ,试求
,试求 的取值范围.
的取值范围. 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
. 的表达式;
的表达式; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 是边长为
是边长为 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
. 最大,试问
最大,试问 应取何值?
应取何值? 最大,试问
最大,试问

 (
( 是自然对数的底数,
是自然对数的底数, ),且
),且 .
. 的值,并求函数
的值,并求函数 的单调区间;
的单调区间; ,对任意
,对任意 ,恒有
,恒有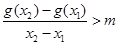 成立.求实数
成立.求实数 的取值范围;
的取值范围;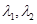 满足
满足 ,
, ,试证明:
,试证明: ;并进一步判断:当正实数
;并进一步判断:当正实数 满足
满足
 ,且
,且 是互不相等的实数时,不等式
是互不相等的实数时,不等式
 是否仍然成立.
是否仍然成立. ,
, 的图象可能是下列图象中的( )
的图象可能是下列图象中的( )
 满足:
满足: ,则
,则 =__________.
=__________. ”的单调递增函数是( )
”的单调递增函数是( )



 ,
,
 ,
, ,记
,记 ,
, 则( )
则( )