Question

【题目】已知定义在R上的函数f（x）满足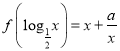 为常数

（1）求函数f（x）的表达式；

（2）如果f（x）为偶函数，求a的值；

（3）当f（x）为偶函数时，若方程f（x）=m有两个实数根x1，x2；其中x1＜0，0＜x2＜1；求实数m的范围．

Answer 1

【答案】（1）f（x）=2﹣x+a2x；（2）1（3）

【解析】解：（1）f(x)=x+,a是常数，令t=x,则x=,

∴f（t）==2﹣t+a2t 从而有f（x）=2﹣x+a2x；

（2）∵f（x）为偶函数，∴f（﹣x）=f（x）

∴2x+a2﹣x=2﹣x+a2x整理可得，（a﹣1）2x=（a﹣1）2﹣x

∴a=1

（3）由（2）可得f（x）为偶函数，a=1，f（x）=2x+2﹣x

令n=2x，n＞0，f（n）=n+，n＞0的图象如图，

结合图象可得方程f（x）=m有两个实数根x1，x2，

其中x1＜0，0＜x2＜1f（n）=m有两个实数根n1，n2其中0＜n1＜1，1＜n2＜2

而函数f（n）=n+在（0，1）上单调递减，在（1，2）单调递增

结合图象可得，函数有两个交点