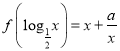ƒøƒ⁄»ð
°æƒø°ø’≈¿œ ¶ø™≥µ…œ∞ý£¨”–¬∑œþ¢Ÿ”ά∑œþ¢⁄¡ΩÃı¬∑œþø…π©—°‘Ò. ¬∑œþ¢Ÿ£∫—ÿÕæ”–![]() ¡Ω¥¶∂¿¡¢‘À––µƒΩªÕ®–≈∫≈µ∆£¨«“¡Ω¥¶”ˆµΩ¬Ãµ∆µƒ∏≈¬ “¿¥ŒŒ™
¡Ω¥¶∂¿¡¢‘À––µƒΩªÕ®–≈∫≈µ∆£¨«“¡Ω¥¶”ˆµΩ¬Ãµ∆µƒ∏≈¬ “¿¥ŒŒ™![]() £¨»Ù
£¨»Ù![]() ¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰2∑÷÷”£ª»Ù
¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰2∑÷÷”£ª»Ù![]() ¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰3∑÷÷”£ª»Ù¡Ω¥¶∂º”ˆ¬Ãµ∆£¨‘Ú»´≥ÃÀ˘ª® ±º‰Œ™20∑÷÷”.
¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰3∑÷÷”£ª»Ù¡Ω¥¶∂º”ˆ¬Ãµ∆£¨‘Ú»´≥ÃÀ˘ª® ±º‰Œ™20∑÷÷”.
¬∑œþ¢⁄£∫—ÿÕæ”–![]() ¡Ω¥¶∂¿¡¢‘À––µƒΩªÕ®–≈∫≈µ∆£¨«“¡Ω¥¶”ˆµΩ¬Ãµ∆µƒ∏≈¬ “¿¥ŒŒ™
¡Ω¥¶∂¿¡¢‘À––µƒΩªÕ®–≈∫≈µ∆£¨«“¡Ω¥¶”ˆµΩ¬Ãµ∆µƒ∏≈¬ “¿¥ŒŒ™![]() £¨»Ù
£¨»Ù![]() ¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰8∑÷÷”£ª»Ù
¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰8∑÷÷”£ª»Ù![]() ¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰5∑÷÷”£ª»Ù¡Ω¥¶∂º”ˆ¬Ãµ∆£¨‘Ú»´≥ÃÀ˘ª® ±º‰Œ™15∑÷÷”.
¥¶”ˆ∫ϵ∆ªÚª∆µ∆£¨‘Úµº÷¬—”ŒÛ ±º‰5∑÷÷”£ª»Ù¡Ω¥¶∂º”ˆ¬Ãµ∆£¨‘Ú»´≥ÃÀ˘ª® ±º‰Œ™15∑÷÷”.
£®1£©»Ù’≈¿œ ¶—°‘Ò¬∑œþ¢Ÿ£¨«ÛÀ˚20∑÷÷”ƒÐµΩ–£µƒ∏≈¬ £ª
£®2£©Œ™ π’≈¿œ ¶»’≥£…œ∞ýÕæ÷–À˘ª® ±º‰Ωœ…Ÿ£¨ƒ„Ω®“È’≈¿œ ¶—°‘ÒƒƒÃı¬∑œþ£ø≤¢Àµ√˜¿Ì”….
°æ¥∞∏°ø(1) ![]() £ª(2)¥∞∏º˚Ω‚Œˆ.
£ª(2)¥∞∏º˚Ω‚Œˆ.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫
(1)¬˙◊„“‚ ±’≈¿œ ¶‘⁄![]() ¡Ω¥¶æ˘”ˆµΩ¬Ãµ∆£¨Ω·∫œ∏≈¬ ≥À∑®π´ Ωø…µ√∏≈¬ ÷µŒ™
¡Ω¥¶æ˘”ˆµΩ¬Ãµ∆£¨Ω·∫œ∏≈¬ ≥À∑®π´ Ωø…µ√∏≈¬ ÷µŒ™![]() £ª
£ª
(2)…Ë—°‘Ò¬∑œþ¢Ÿµƒ—”ŒÛ ±º‰Œ™Àʪ˙±‰¡ø![]() ,—°‘Ò¬∑œþ¢⁄µƒ—”ŒÛ ±º‰Œ™Àʪ˙±‰¡ø
,—°‘Ò¬∑œþ¢⁄µƒ—”ŒÛ ±º‰Œ™Àʪ˙±‰¡ø![]() £¨º∆À„œý”¶µƒ ˝—ß∆⁄Õ˚ø…µ√
£¨º∆À„œý”¶µƒ ˝—ß∆⁄Õ˚ø…µ√![]() £¨
£¨ ![]() £¨æð¥ÀΩ®“È’≈¿œ ¶—°‘Ò¬∑œþ¢⁄.
£¨æð¥ÀΩ®“È’≈¿œ ¶—°‘Ò¬∑œþ¢⁄.
‘Ã‚Ω‚Œˆ£∫
£®1£©◊þ¬∑œþ¢Ÿ£¨20∑÷÷”ƒÐµΩ–£“‚Œ∂◊≈’≈¿œ ¶‘⁄![]() ¡Ω¥¶æ˘”ˆµΩ¬Ãµ∆£¨º«∏√ ¬º˛Œ™
¡Ω¥¶æ˘”ˆµΩ¬Ãµ∆£¨º«∏√ ¬º˛Œ™![]() £¨‘Ú
£¨‘Ú![]() .
.
£®2£©…Ë—°‘Ò¬∑œþ¢Ÿµƒ—”ŒÛ ±º‰Œ™Àʪ˙±‰¡ø![]() ,‘Ú
,‘Ú![]() µƒÀ˘”–ø…ƒÐ»°÷µ Œ™ 0£¨ 2£¨ 3£¨ 5.
µƒÀ˘”–ø…ƒÐ»°÷µ Œ™ 0£¨ 2£¨ 3£¨ 5.
‘Ú![]() £¨
£¨
![]() .
.
![]() µƒ ˝—ß∆⁄Õ˚
µƒ ˝—ß∆⁄Õ˚![]() .
.
…Ë—°‘Ò¬∑œþ¢⁄µƒ—”ŒÛ ±º‰Œ™Àʪ˙±‰¡ø![]() £¨‘Ú
£¨‘Ú![]() µƒø…ƒÐ»°÷µŒ™0£¨ 8£¨ 5£¨ 13.
µƒø…ƒÐ»°÷µŒ™0£¨ 8£¨ 5£¨ 13.
‘Ú![]() £¨
£¨
![]() .
.
![]() µƒ ˝—ß∆⁄Õ˚
µƒ ˝—ß∆⁄Õ˚![]() .
.
“Ú¥À—°‘Ò¬∑œþ¢Ÿ∆Ωæ˘À˘ª® ±º‰Œ™![]() ∑÷÷”£¨—°‘Ò¬∑œþ¢⁄∆Ωæ˘À˘ª® ±º‰Œ™
∑÷÷”£¨—°‘Ò¬∑œþ¢⁄∆Ωæ˘À˘ª® ±º‰Œ™![]() ∑÷÷”£¨
∑÷÷”£¨
À˘“‘Œ™ π’≈¿œ ¶»’≥£…œ∞ýÕæ÷–À˘ª® ±º‰Ωœ…Ÿ£¨Ω®“È’≈¿œ ¶—°‘Ò¬∑œþ¢⁄.