题目内容
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点
的焦点![]() 重合,且点
重合,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
, ![]() 与
与![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的方程为
的方程为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据抛物线的几何性质,求解![]() 的值,进而得到椭圆的焦点坐标,即
的值,进而得到椭圆的焦点坐标,即![]() ,又由两曲线的公共点的坐标,代入椭圆的方程,即可求得
,又由两曲线的公共点的坐标,代入椭圆的方程,即可求得![]() 的值,得到椭圆的方程;
的值,得到椭圆的方程;
(2)当![]() 过点
过点![]() 且垂直于
且垂直于![]() 轴时,此时
轴时,此时![]() 的方程为
的方程为![]() 代入椭圆的方程,求得
代入椭圆的方程,求得![]() ,进而求得此时
,进而求得此时![]() 的值,当
的值,当![]() 与
与![]() 轴不垂直时,可设
轴不垂直时,可设![]() 的方程为
的方程为![]() ,
,
设![]() ,代入椭圆的方程,利用根与系数的关系及韦达定理的应用,化简即可求解
,代入椭圆的方程,利用根与系数的关系及韦达定理的应用,化简即可求解![]() 的值。
的值。
试题解析:(1)∵![]() 的焦点
的焦点![]() 的坐标为
的坐标为![]() ,
,
由点![]() 到直线
到直线![]() 的距离为
的距离为![]() 得
得 .
.
∵![]() ,解得
,解得![]() ,又
,又![]() 为椭圆的一个焦点,∴
为椭圆的一个焦点,∴![]() .
.
∵![]() 与
与![]() 的公共弦长为
的公共弦长为![]() ,
, ![]() 与
与![]() 都关于
都关于![]() 轴对称,
轴对称,
而![]() 的方程为
的方程为![]() ,从而
,从而![]() 与
与![]() 的公共点的坐标为
的公共点的坐标为![]() ,
,
∴![]() ②,
②,
联立①②解得![]() ,
,
∴![]() 的方程为
的方程为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(2)当![]() 过点
过点![]() 且垂直于
且垂直于![]() 轴时,
轴时, ![]() 的方程为
的方程为![]() 代入
代入![]() 求得
求得![]() ,
,
∴![]() ,把
,把![]() 代入
代入![]() 求得
求得![]() ,∴
,∴![]() ,
,
此时![]() .
.
当![]() 与
与![]() 轴不垂直时,要使
轴不垂直时,要使![]() 与
与![]() 有两个交点,可设
有两个交点,可设![]() 的方程为
的方程为![]() ,
,
此时设![]()
把直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立得
的方程联立得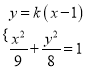 ,
,
消去![]() 化简得
化简得![]() ,
,
可得![]() ,
,
∴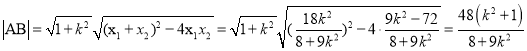 ,
,
把直线![]() 的方程与抛物线
的方程与抛物线![]() 的方程联立得
的方程联立得![]() ,
,
消去![]() 化简得
化简得![]() ,
,
可得![]() ,
,
∴![]() ,
,
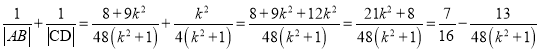 ,
,
∵![]() ,∴
,∴![]() ,∴
,∴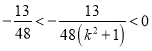 ,
,
∴![]() ,
,
综上可得![]() 的取值范围是
的取值范围是![]()

【题目】2017年“一带一路”国际合作高峰论坛于今年5月14日至15日在北京举行.为高标准完成高峰论坛会议期间的志愿服务工作,将从27所北京高校招募大学生志愿者,某调查机构从是否有意愿做志愿者在某高校访问了80人,经过统计,得到如下丢失数据的列联表:(![]() ,表示丢失的数据)
,表示丢失的数据)
无意愿 | 有意愿 | 总计 | |
男 |
|
| 40 |
女 | 5 |
|
|
总计 | 25 |
| 80 |
(1)求出![]() 的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
的值,并判断:能否有99.9%的把握认为有意愿做志愿者与性别有关;
(2)若表中无意愿做志愿者的5个女同学中,3个是大学三年级同学,2个是大学四年级同学.现从这5个同学中随机选2同学进行进一步调查,求这2个同学是同年级的概率.
附参考公式及数据: 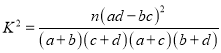 ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i) | 分组睡眠时间 | 组中值(mi) | 频数(人数) | 频率(fi) |
1 | [4,5) | 4.5 | 80 | |
2 | [5,6) | 5.5 | 520 | 0.26 |
3 | [6,7) | 6.5 | 600 | 0.30 |
4 | [7,8) | 7.5 | ||
5 | [8,9) | 8.5 | 200 | 0.10 |
6 | [9,10] | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
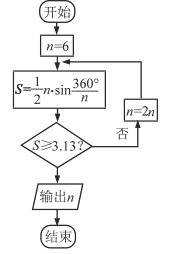
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.
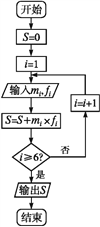
【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.