题目内容
13.把下列各角的度数化为弧度数,并写成0到2π的角加上2kπ(k∈Z)的形式:(1)-64°;
(2)400°;
(3)-722°30′.
分析 由1$°=\frac{π}{180}$,把各角化为弧度制,然后化为0到2π的角加上2kπ(k∈Z)的形式得答案.
解答 解:(1)-64°=-$64×\frac{π}{180}$=$-\frac{16π}{45}$=$-2π+\frac{74π}{45}$;
(2)400°=400×$\frac{π}{180}$=$2π+\frac{2π}{9}$;
(3)-722°30′=-722.5×$\frac{π}{180}$=$-6π+\frac{715π}{360}$.
点评 本题考查终边相同的角,考查了角度制与弧度制的互化,考查运算能力,是基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
3.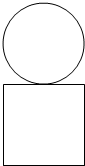 某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
 某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )| A. | 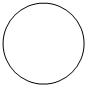 | B. |  | C. | 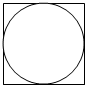 | D. |  |
3.已知$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,|$\overrightarrow{AB}$|=$\frac{1}{t}$,|$\overrightarrow{AC}$|=t,t∈[$\frac{1}{4}$,4];若P是△ABC所在平面内一点,且$\overrightarrow{AP}$=$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{4\overrightarrow{AC}}{|\overrightarrow{AC}|}$,则$\overrightarrow{PB}$$•\overrightarrow{PC}$的取值范围是( )
| A. | [13,17] | B. | [12,13] | C. | [$\frac{3}{4}$,12] | D. | [$\frac{3}{4}$,13] |