题目内容
14.已知过点M(-3,0)的直线l被圆x2+(y+2)2=25所截得的弦长为8,那么直线l的方程为x=-3或5x-12y+15=0.分析 设直线方程为y=k(x+3)或x=-3,根据直线l被圆圆x2+(y+2)2=25所截得的弦长为8,可得圆心到直线的距离为3,利用点到直线的距离公式确定k值,验证x=-3是否符合题意.
解答 解:设直线方程为y=k(x+3)或x=-3,
∵圆心坐标为(0,-2),圆的半径为5,
∴圆心到直线的距离d=$\sqrt{25-16}$=3,
∴$\frac{|3k+2|}{\sqrt{1+{k}^{2}}}$=3,
∴k=$\frac{5}{12}$,∴直线方程为y=$\frac{5}{12}$(x+3),即5x-12y+15=0;
直线x=-3,圆心到直线的距离d=|-3|=3,符合题意,
故答案为:x=-3或5x-12y+15=0.
点评 本题考查了待定系数法求直线方程,考查了直线与圆相交的相交弦长公式,注意不要漏掉x=-3.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
5.已知函数f(x)=x2-cosx,则$f(\frac{3}{5}),f(0),f(-\frac{1}{2})$的大小关系是( )
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
2.设i为虚数单位,则|1-i|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
9.若变量x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y-4≤0}\\{x-y≤0}\end{array}\right.$,则$\frac{y}{x}$的最大值为( )
| A. | 2 | B. | 3 | C. | $\frac{4}{3}$ | D. | 5 |
3.下列程序框图的功能是寻找使2×4×6×8×…×i>2015成立的i的最小正整数值,则输出框中应填( )
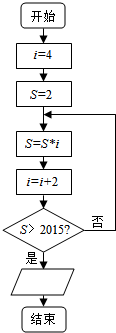

| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |

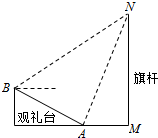 2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.
2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.