题目内容
【题目】已知椭圆C: ![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且过点
的离心率互为倒数,且过点![]() .
.
(1)求椭圆C的方程;
(2)过![]() 作两条直线
作两条直线![]() 与圆
与圆![]() 相切且分别交椭圆于M、N两点.
相切且分别交椭圆于M、N两点.
① 求证:直线MN的斜率为定值;
② 求△MON面积的最大值(其中O为坐标原点).
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】试题分析:(1)先求双曲线离心率得椭圆离心率,再将点坐标代入椭圆方程,解方程组得![]() ,(2)①先根据点斜式得直线
,(2)①先根据点斜式得直线![]() 方程,再与椭圆方程联立解得
方程,再与椭圆方程联立解得![]() 坐标,根据直线
坐标,根据直线![]() 与圆
与圆![]() 相切,得斜率相反,同理可得
相切,得斜率相反,同理可得![]() 最后根据斜率公式求斜率,②设直线MN方程,根据原点到直线距离得高,与椭圆方程联立方程组结合韦达定理以及弦长公式得底边边长,最后代入三角形面积公式,利用基本不等式求最值.
最后根据斜率公式求斜率,②设直线MN方程,根据原点到直线距离得高,与椭圆方程联立方程组结合韦达定理以及弦长公式得底边边长,最后代入三角形面积公式,利用基本不等式求最值.
试题解析:(1)可得![]() ,设椭圆的半焦距为
,设椭圆的半焦距为![]() ,所以
,所以![]() ,
,
因为C过点![]() ,所以
,所以![]() ,又
,又![]() ,解得
,解得![]() ,
,
所以椭圆方程为![]() .
.
(2)① 显然两直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,
, ![]() ,
,
由于直线![]() 与圆
与圆![]() 相切,则有
相切,则有![]() ,
,
直线![]() 的方程为
的方程为![]() , 联立方程组
, 联立方程组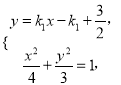
消去![]() ,得
,得![]() ,
,
因为![]() 为直线与椭圆的交点,所以
为直线与椭圆的交点,所以![]() ,
,
同理,当![]() 与椭圆相交时,
与椭圆相交时, ![]() ,
,
所以![]() ,而
,而![]() ,
,
所以直线![]() 的斜率
的斜率![]() .
.
② 设直线![]() 的方程为
的方程为![]() ,联立方程组
,联立方程组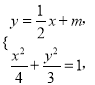 消去
消去![]() 得
得![]() ,
,
所以 ,
,
原点![]() 到直线的距离
到直线的距离![]() ,
,
![]() 面积为
面积为![]() ,
,
当且仅当![]() 时取得等号.经检验,存在
时取得等号.经检验,存在![]() (
(![]() ),使得过点
),使得过点![]() 的两条直线与圆
的两条直线与圆![]() 相切,且与椭圆有两个交点M,N.
相切,且与椭圆有两个交点M,N.
所以![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目