题目内容
12.一个盒中有9个正品和3个次品,每次取一个零件,如果取出是次品就不再放回,求在以取得正品前,已知得次品数概率x的分布列,并求P($\frac{1}{2}$≤x≤$\frac{5}{2}$).分析 x所有可能取的值为0,1,2,3,分别求出P(x=0),P(x=1),P(x=2),P(x=3),从而求出分布列,以及满足条件的概率值.
解答 解:显然x所有可能取的值为0,1,2,3.
∵P(x=0)=$\frac{9}{12}$=$\frac{3}{4}$,
P(x=1)=$\frac{3}{12}$×$\frac{9}{11}$=$\frac{9}{44}$,
P(x=2)=$\frac{3}{12}$×$\frac{2}{11}$×$\frac{9}{10}$=$\frac{9}{220}$,
P(x=3)=$\frac{3}{12}$×$\frac{2}{11}$×$\frac{1}{10}$×$\frac{9}{9}$=$\frac{1}{220}$,
∴x的分布列是:
| x | 0 | 1 | 2 | 3 |
| P | $\frac{3}{4}$ | $\frac{9}{44}$ | $\frac{9}{220}$ | $\frac{1}{220}$ |
点评 本题考查离散型随机变量的分布列,是基础题.解题时要认真审题,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想.

练习册系列答案
相关题目
20.为了了解两种手机电池的待机时间,研究人员分别对甲、乙两种电池做了7次测试,测试结果统计如下表所示:
(Ⅰ)试计算7次测试中,甲、乙两种电池的待机时间的平均值和方差,并判断哪种电池的性能比较好,简单说明理由.
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.
| 测试次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 甲电池待机时间(h) | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
| 乙电池待机时间(h) | 118 | 123 | 127 | 120 | 124 | 120 | 122 |
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.
 设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.
设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.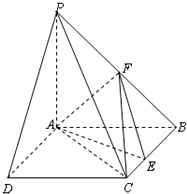 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动. 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC.
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC. 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B,F分别为DE,BC中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B,F分别为DE,BC中点. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,且过点(1,$\frac{{\sqrt{6}}}{3}$).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,且过点(1,$\frac{{\sqrt{6}}}{3}$). 如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.
如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6. 如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为$\frac{\sqrt{3}}{2}$,两条准线之间的距离为$\frac{8\sqrt{3}}{3}$.B,C分别为椭圆M的上、下顶点,过点T(t,2)(t≠0)的直线TB,TC分别与椭圆M交于E,F两点.
如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为$\frac{\sqrt{3}}{2}$,两条准线之间的距离为$\frac{8\sqrt{3}}{3}$.B,C分别为椭圆M的上、下顶点,过点T(t,2)(t≠0)的直线TB,TC分别与椭圆M交于E,F两点.