题目内容
10.已知四面体A-BCD满足下列条件:(1)有一个面是边长为1的等边三角形;
(2)有两个面是等腰直角三角形.
那么四面体A-BCD的体积的取值集合是( )
| A. | $\{\frac{1}{2},\frac{{\sqrt{2}}}{12}\}$ | B. | $\{\frac{1}{6},\frac{{\sqrt{3}}}{12}\}$ | C. | $\{\frac{{\sqrt{2}}}{12},\frac{{\sqrt{3}}}{12},\frac{{\sqrt{2}}}{24}\}$ | D. | $\{\frac{1}{6},\frac{{\sqrt{2}}}{12},\frac{{\sqrt{2}}}{24}\}$ |
分析 由题意,分类讨论,(1)△BCD是等边三角形,BA⊥AC,DA⊥AC;(2)△BCD是等边三角形,BA⊥BD,BA⊥BC;△BCD是等边三角形,BA⊥BD,DC⊥AC,求出体积即可.
解答 解:由题意,分类讨论可得
(1)△BCD是等边三角形,BA⊥AC,DA⊥AC,所以四面体A-BCD的体积为$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{24}$;
(2)△BCD是等边三角形,BA⊥BD,BA⊥BC,所以四面体A-BCD的体积为$\frac{1}{3}×\frac{\sqrt{3}}{4}×1$=$\frac{\sqrt{3}}{12}$;
(3)△BCD是等边三角形,BA⊥BD,DC⊥AC,取AD的中点O,可得BO=DO=$\frac{\sqrt{2}}{2}$,所以四面体A-BCD的体积为$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}×\sqrt{2}$=$\frac{\sqrt{2}}{12}$.
故选:C.
点评 本题考查三棱锥体积的计算,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.为了了解两种手机电池的待机时间,研究人员分别对甲、乙两种电池做了7次测试,测试结果统计如下表所示:
(Ⅰ)试计算7次测试中,甲、乙两种电池的待机时间的平均值和方差,并判断哪种电池的性能比较好,简单说明理由.
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.
| 测试次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 甲电池待机时间(h) | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
| 乙电池待机时间(h) | 118 | 123 | 127 | 120 | 124 | 120 | 122 |
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.
 如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.
如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6. 如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为$\frac{\sqrt{3}}{2}$,两条准线之间的距离为$\frac{8\sqrt{3}}{3}$.B,C分别为椭圆M的上、下顶点,过点T(t,2)(t≠0)的直线TB,TC分别与椭圆M交于E,F两点.
如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其离心率为$\frac{\sqrt{3}}{2}$,两条准线之间的距离为$\frac{8\sqrt{3}}{3}$.B,C分别为椭圆M的上、下顶点,过点T(t,2)(t≠0)的直线TB,TC分别与椭圆M交于E,F两点.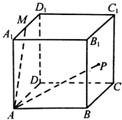 在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面BCC1B1上运动.现有下列命题:
在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面BCC1B1上运动.现有下列命题: